Gráficos espaciales

Hay dos grandes tipos de datos espaciales: grillas regulares y grillas irregulares.

Grillas regulares

En la segunda sección de lectura de datos viste cómo leer archivos NetCDF:

temperatura <- ReadNetCDF("datos/temperatura.nc", vars = "air",
                          subset = list(level = 1000,
                                        lat = c(-55, -20),
                                        lon = c(280, 310))) 
glimpse(temperatura)

## Rows: 195
## Columns: 5
## $ time  <dttm> 2010-07-09, 2010-07-09, 2010-07-09, 2010-07-09, 2010-07-09, 201…
## $ level <dbl> 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000, 1000…
## $ lat   <dbl> -20.0, -20.0, -20.0, -20.0, -20.0, -20.0, -20.0, -20.0, -20.0, -…
## $ lon   <dbl> 280.0, 282.5, 285.0, 287.5, 290.0, 292.5, 295.0, 297.5, 300.0, 3…
## $ air   <dbl> 287.62, 287.70, 289.72, 293.25, 296.32, 297.30, 296.57, 296.15, …

La variable temperatura es una tabla que tiene dato de temperatura del aire para cada tiempo, nivel (altura), latitud y longitud. Como este archivo tiene información sólo para un tiempo y el código filtró sólo datos de un nivel, entonces la variación es sólo en latitud y longitud. ¿Cómo se grafica?

Se puede dibujar un punto por cada dato:

ggplot(temperatura, aes(lon, lat)) +
  geom_point()

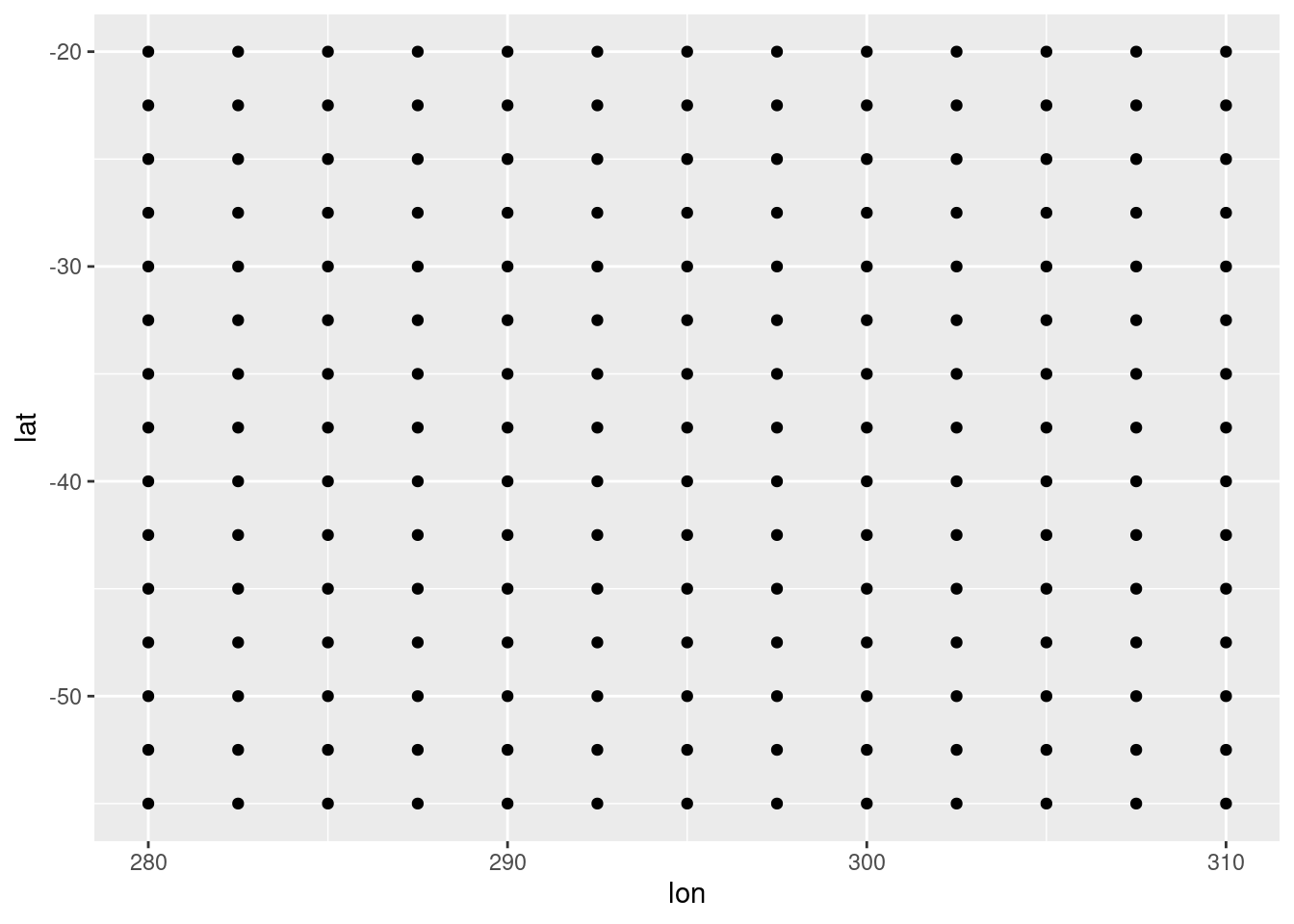
Esto no dice nada, aunque podemos confirmar que los datos están en una grilla regular. Para visualizar la temperatura, hay que mapear éste valor a un parámetro estético, por ejemplo, el color:

ggplot(temperatura, aes(lon, lat)) +
  geom_point(aes(color = air))

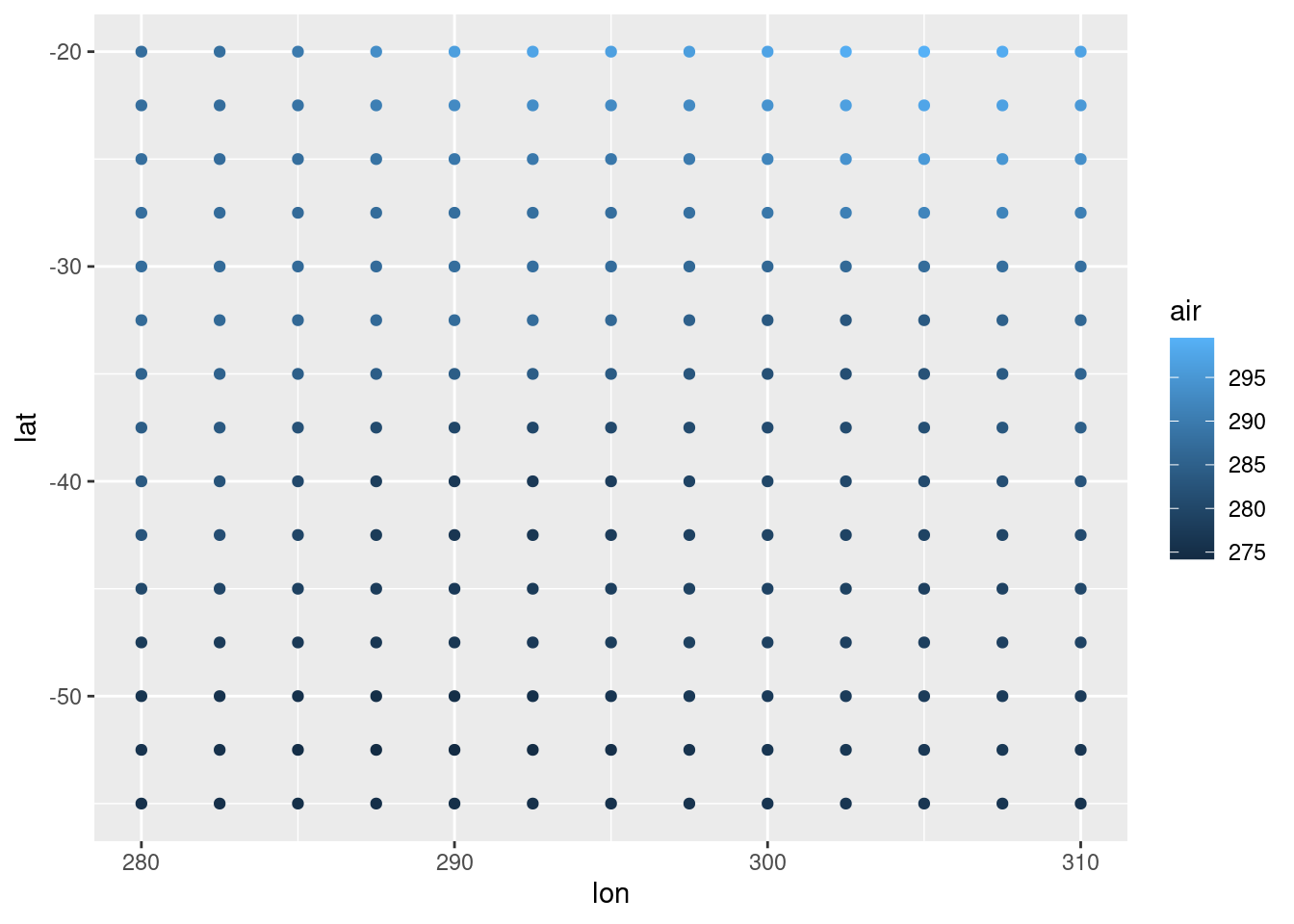
Puntos redondos y separados no es la forma más informativa de ver estos datos. Una grilla regular en realidad define como una “imagen” donde cada punto es un pixel. Esto se llama un “raster” y con ggplot se puede graficar con geom_raster().

ggplot(temperatura, aes(lon, lat)) +
  geom_raster(aes(fill = air))

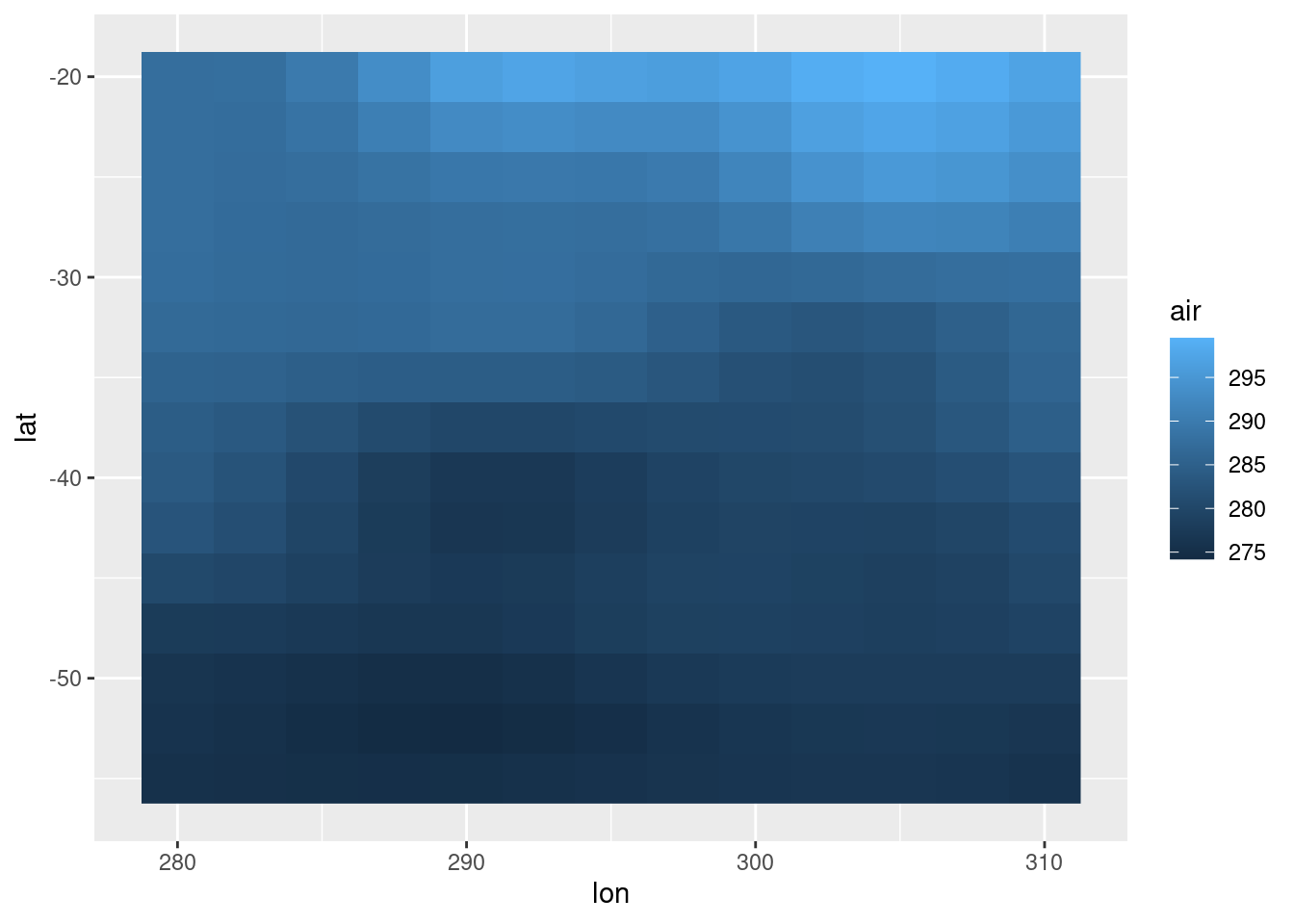
geom_raster() dibuja rectángulos de igual ancho y alto en cada x, y. El ancho y el alto se definen a través de la resolución de los datos. Funcionan perfectamente para grillas regulares. Estos rectángulos tienen un color interno, por lo que el parámetro estético se llama “fill”.

Desafío

ggplot2 tiene tres funciones para generar rectángulos: geom_raster(), geom_tile() y geom_rect(). ¿Cuál es la diferencia entre cada uno? Fijate en la documentación.

Mapas

Bien, hasta ahí tenés un gráfico con los datos, pero para entenderlos en su contexto espacial como mínimo hace falta un mapa. Para tener un mapa se necesitan datos de la localización de las costas o las fronteras. Existen varias fuentes de estos datos, pero una muy buena es Natural Earth. El paquete {rnaturalearth} provee una interfaz amigable para usar estos datos directamente en {ggplot2}.

Primero hay que cargar el mapa que queramos. Por ejemplo, para graficar el mapa de Argentina y sus países limítrofes cargamos los datos con ne_countries():

mapa <- rnaturalearth::ne_countries(country = c("argentina", "chile", "uruguay", 
                                                "paraguay", "brazil", "bolivia", 
                                                "falkland islands"), 
                                    returnclass = "sf")

El argumento country es un vector con los países que necesitamos. El argumento returnclass es un poco técnico, pero hace referencia a la estructura que queremos que devuelva. En este caso, returnclass = "sf" hace que devuelva un objeto de clase “Simple Features”. Las “Simple Features” son cualquier cosa menos simple internamente pero con {ggplot2} se pueden graficar con un geom específico:

ggplot(mapa) +
  geom_sf()

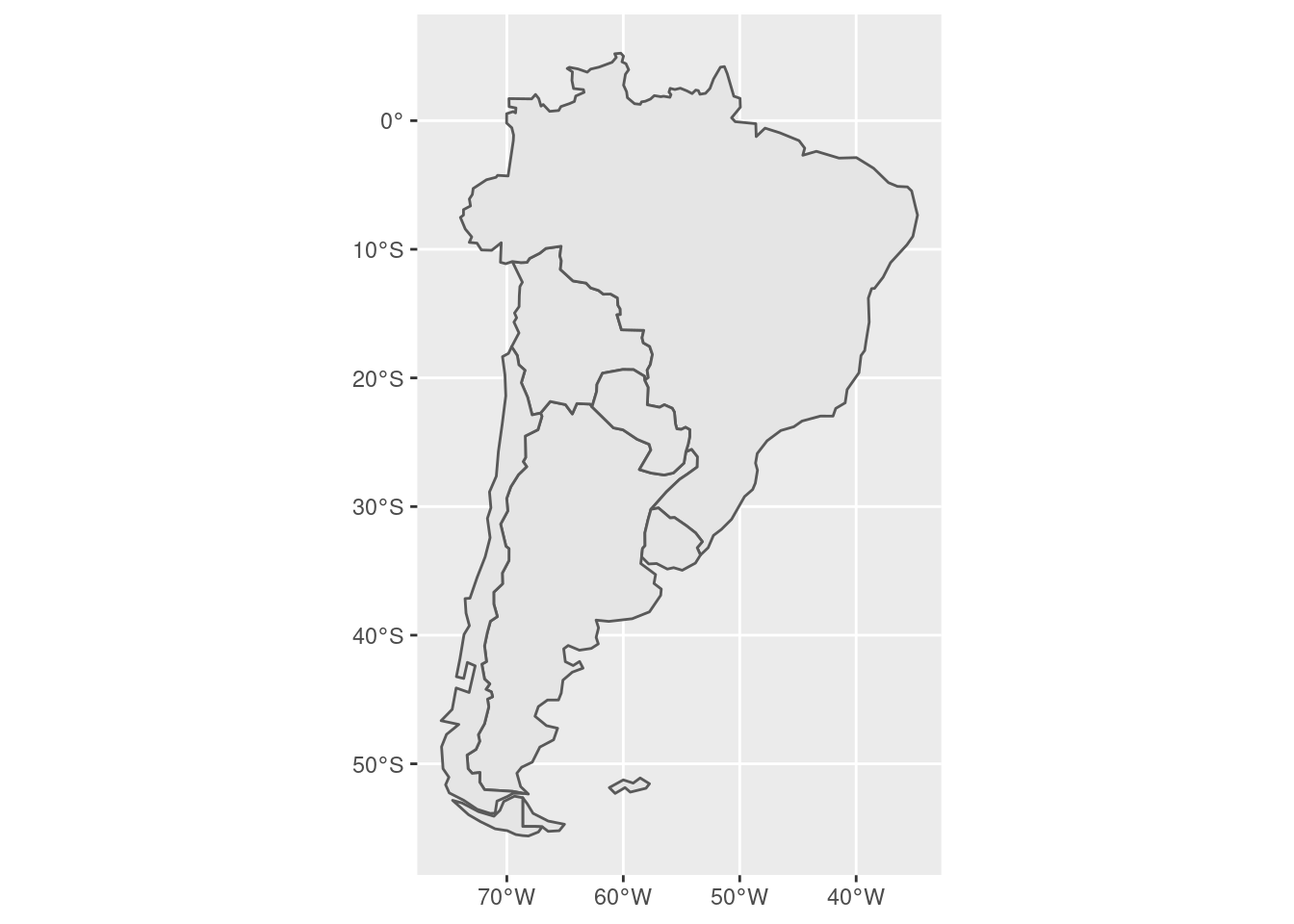
Por defecto, el mapa se dibuja con un fondo gris, pero el problema es ese fondo va a tapar los datos! Paro para dibujar sólo los contornos hay que modificarlo un poco:

ggplot(mapa) +
  geom_sf(fill = NA, color = "black", size = 0.2)

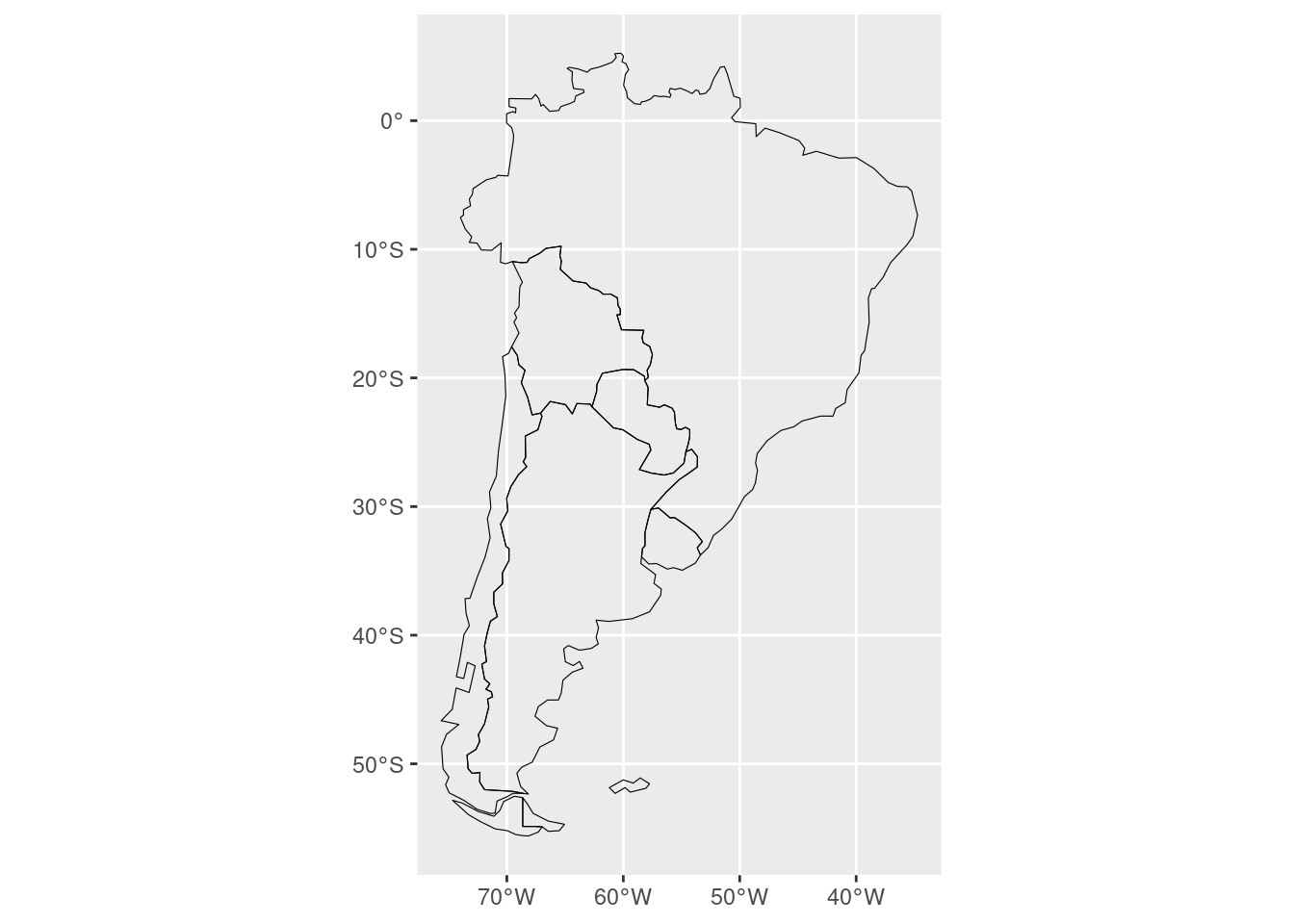
Cuando uno usa mucho un mapa, muchas veces termina siendo útil guardar el geom por separado en una variable.

mi_mapa <- geom_sf(data = mapa, inherit.aes = FALSE, fill = NA, color = "black", size = 0.2) 

Además de las modificaciones estéticas, esta llamada a geom_sf tiene el argumento data = mapa, ya que no va a usar los datos “globales” de la llamada a ggplot(). También tiene ìnherit.aes = FALSE porque tampoco tiene que “heredar” los aes globales.

Entonces ahora, para graficar la temperatura y el mapa encima, armamos el gráfico de raster igual que antes y le sumamos el mapa:

ggplot(temperatura, aes(lon, lat)) +
  geom_raster(aes(fill = air)) +
  mi_mapa

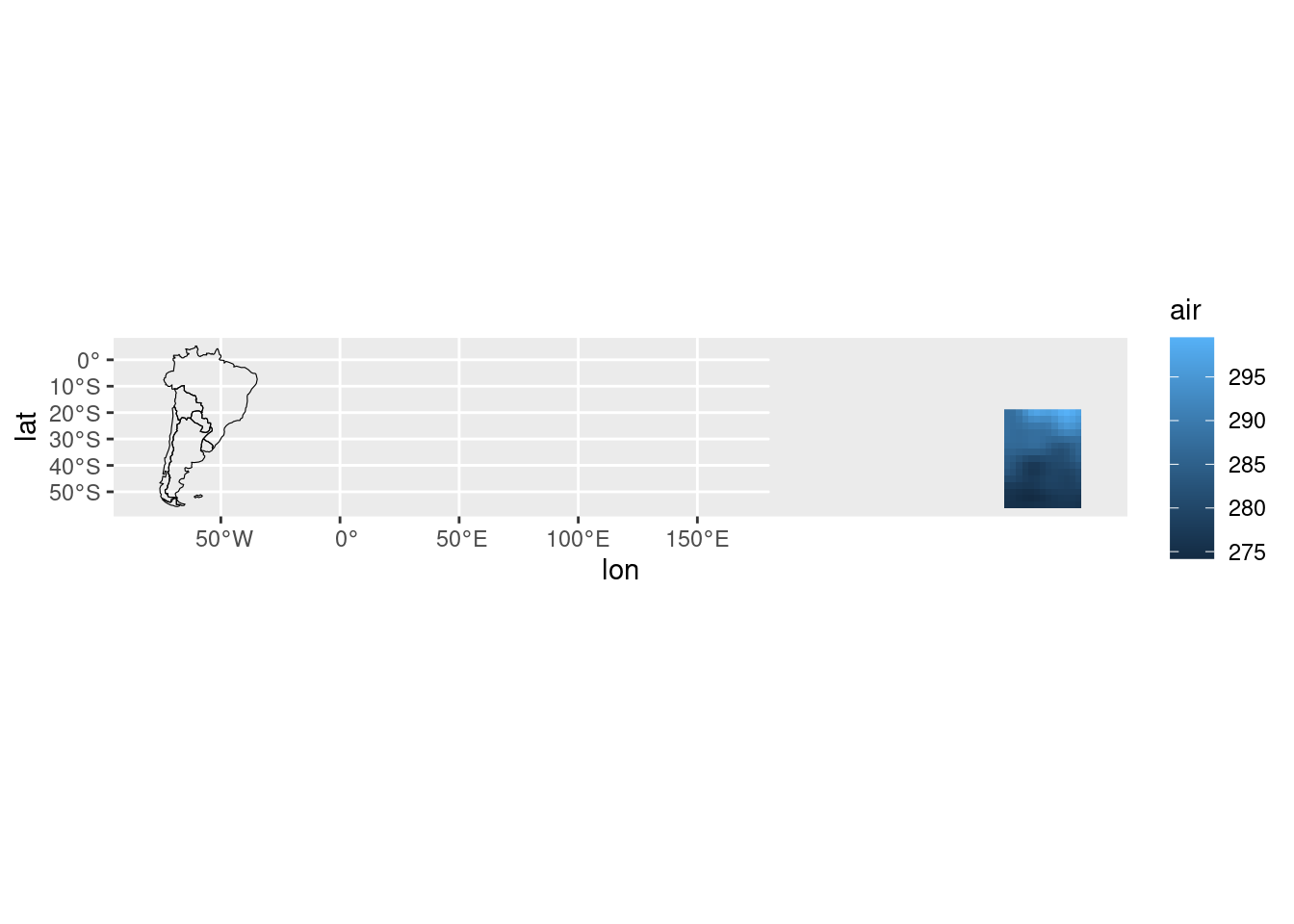
Desafío

¿Podés explicar qué salió mal?

Existen dos convenciones básicas para medir la longitud, medida entre 0º y 360º o entre -180º y +180º. Los datos de temperatura usan la primera y los del mapa, la segunda. Para convertir entre una y otra convención, podés usar la función ConvertLongitude() de {metR}:

temperatura <- mutate(temperatura, lon = metR::ConvertLongitude(lon, from = 360))

ggplot(temperatura, aes(lon, lat)) +
  geom_raster(aes(fill = air)) +
  mi_mapa 

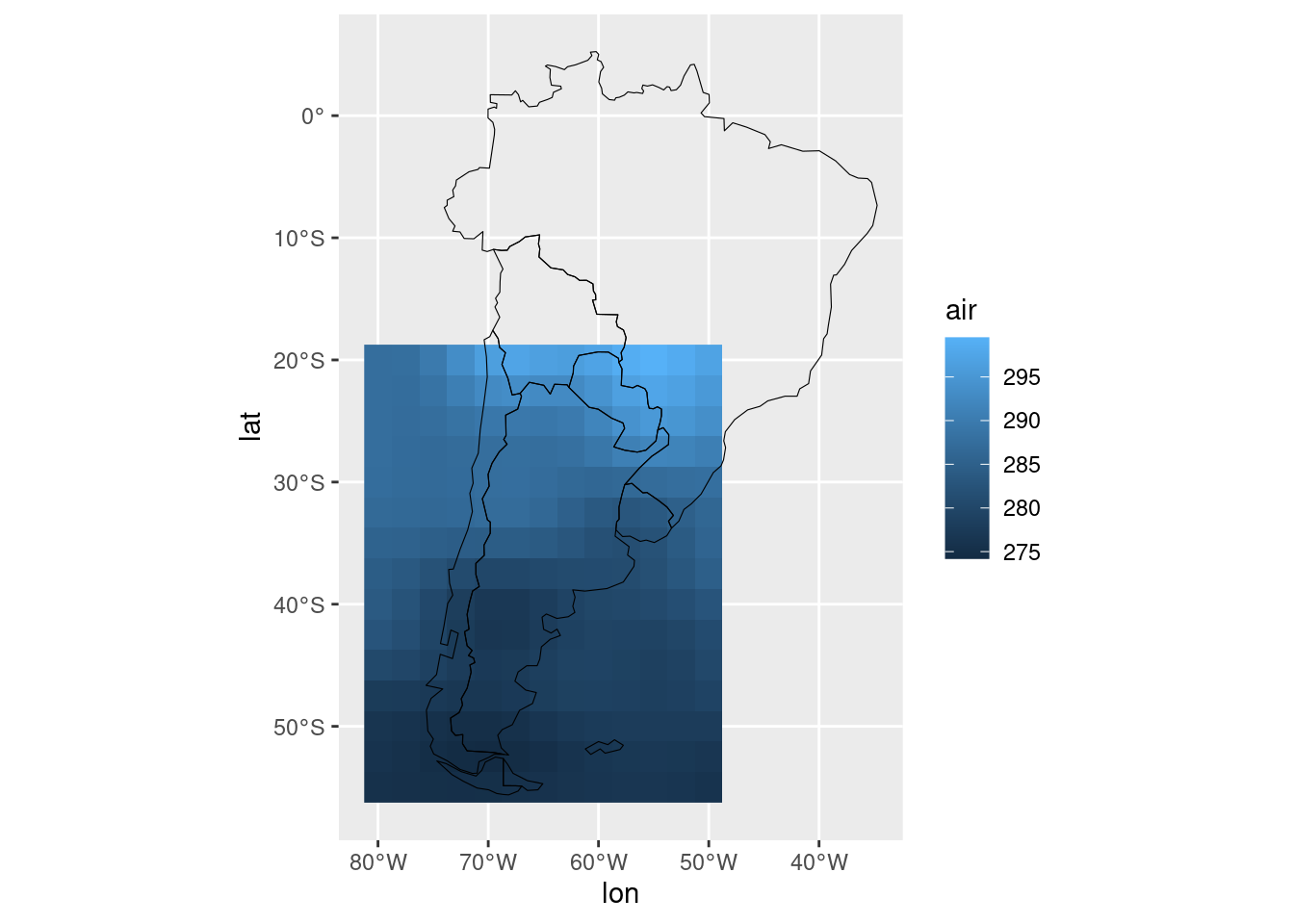
Lo único que le falta a este gráfico es lo que le sobra: todo el espacio donde no hay datos. Para recortar el área del gráfico y que tome sólo donde tenemos datos de temperatura, hay que especificar los límites del sistema de coordenadas. Como mi_mapa es un geom_sf, hay que usar coord_sf.

ggplot(temperatura, aes(lon, lat)) +
  geom_raster(aes(fill = air)) +
  mi_mapa +
  coord_sf(ylim = c(-55, -20), xlim = c(-80, -50))

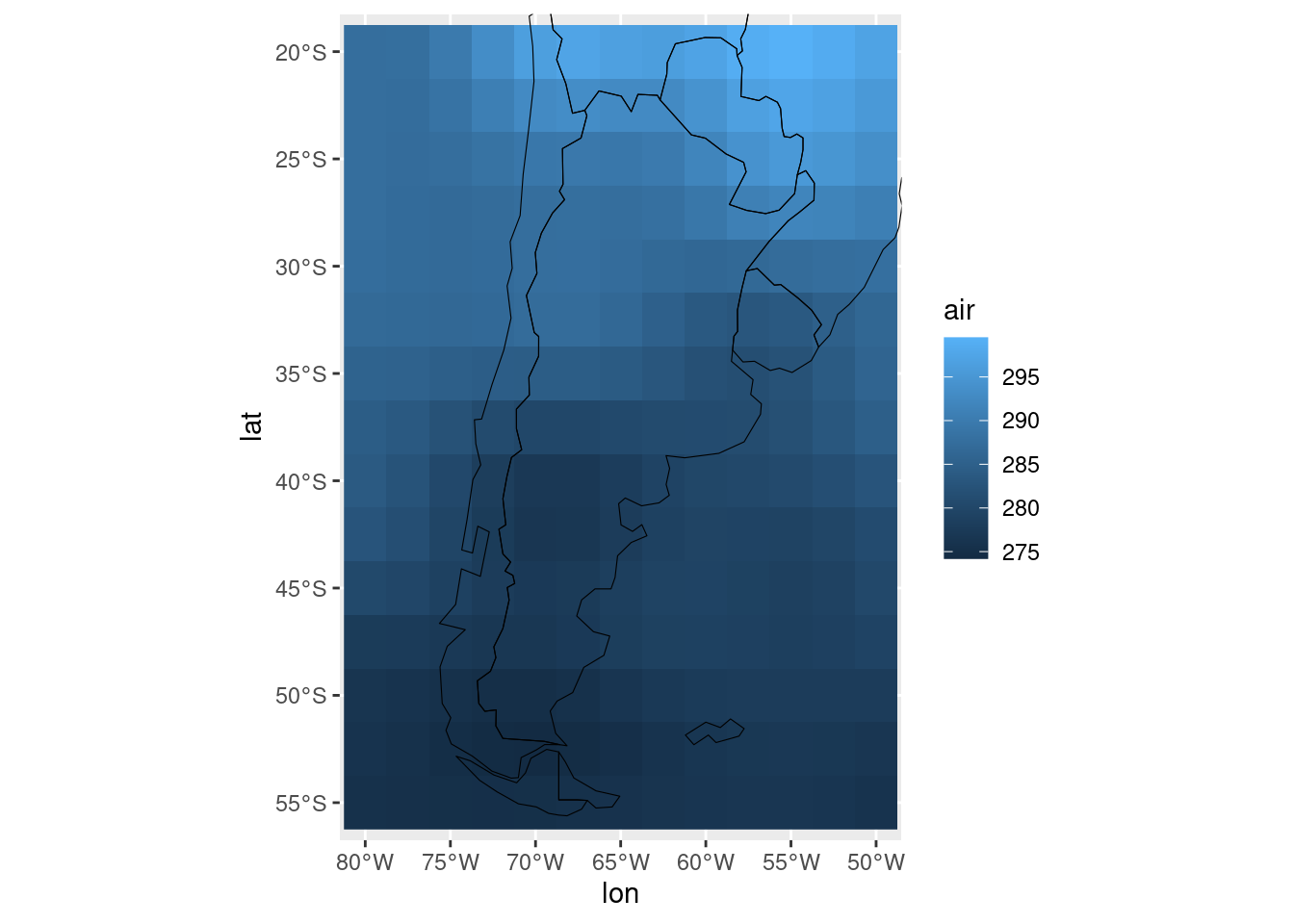
Otra forma de graficar datos espaciales es pensarlos como una superficie tridimensional donde el x y el y son las coordenadas y la altura (la coordenada z) es proporcional al valor de la variable. Imaginándoselo así, este gráfico de temperatura sería una montaña con su cima en Paraguay y su punto más bajo cerca de Chubut.

Precisamente para esta situación están pensadas las líneas de contorno que se pueden graficar en {ggplot2} usando la función geom_contour().

ggplot(temperatura, aes(lon, lat)) +
  geom_contour(aes(z = air)) +
  mi_mapa +
  coord_sf(ylim = c(-55, -20), xlim = c(-80, -50))

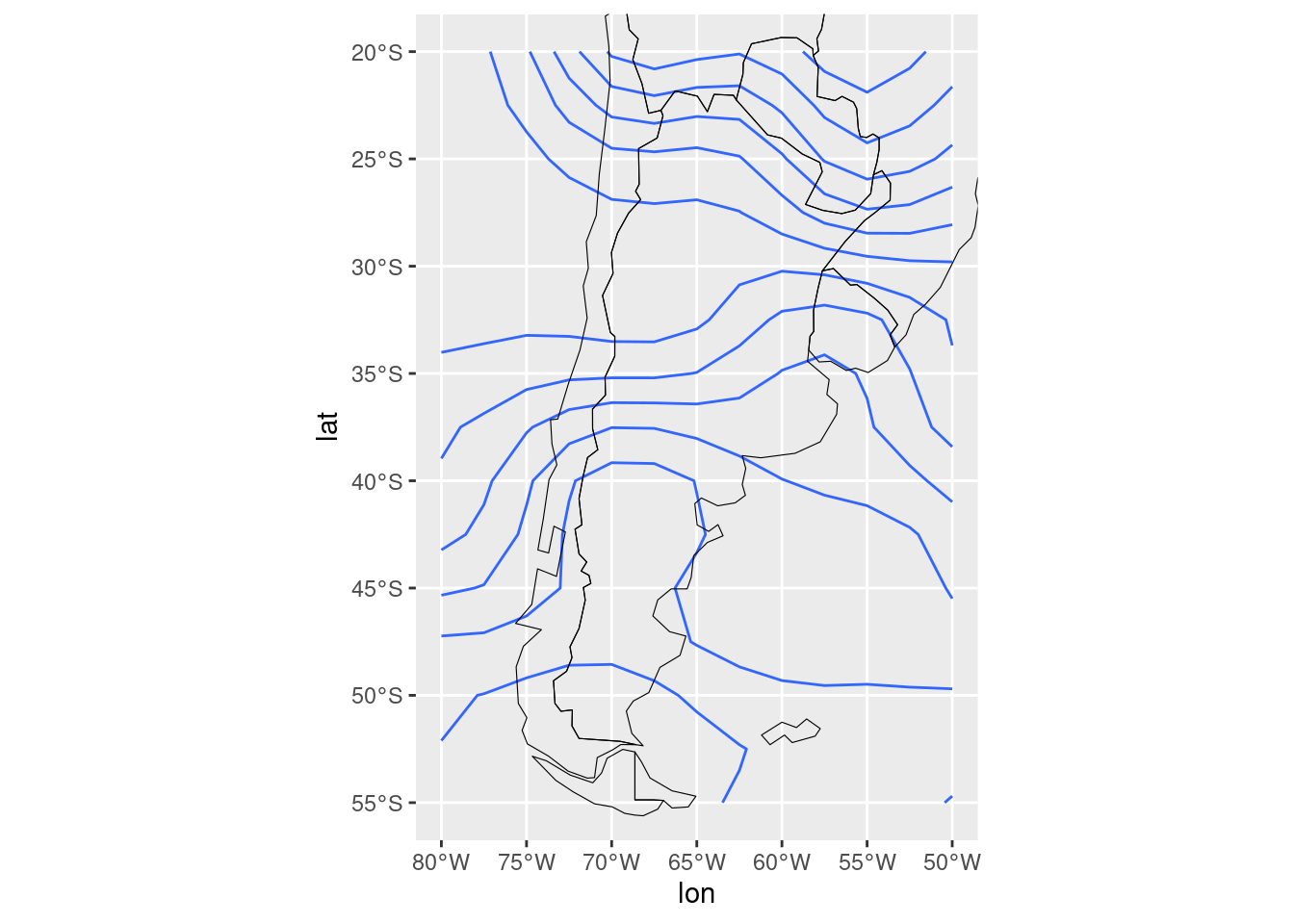
Las líneas dibujadas por geom_contour() son líneas de nivel que unen puntos de valor constante. Sin embargo, esas líneas azules no dan ninguna indicación del valor de la variable por lo que es conveniente mapear el color de las líneas ese valor constante.

ggplot(temperatura, aes(lon, lat)) +
  geom_contour(aes(z = air, color = stat(level))) +
  mi_mapa +
  coord_sf(ylim = c(-55, -20), xlim = c(-80, -50))

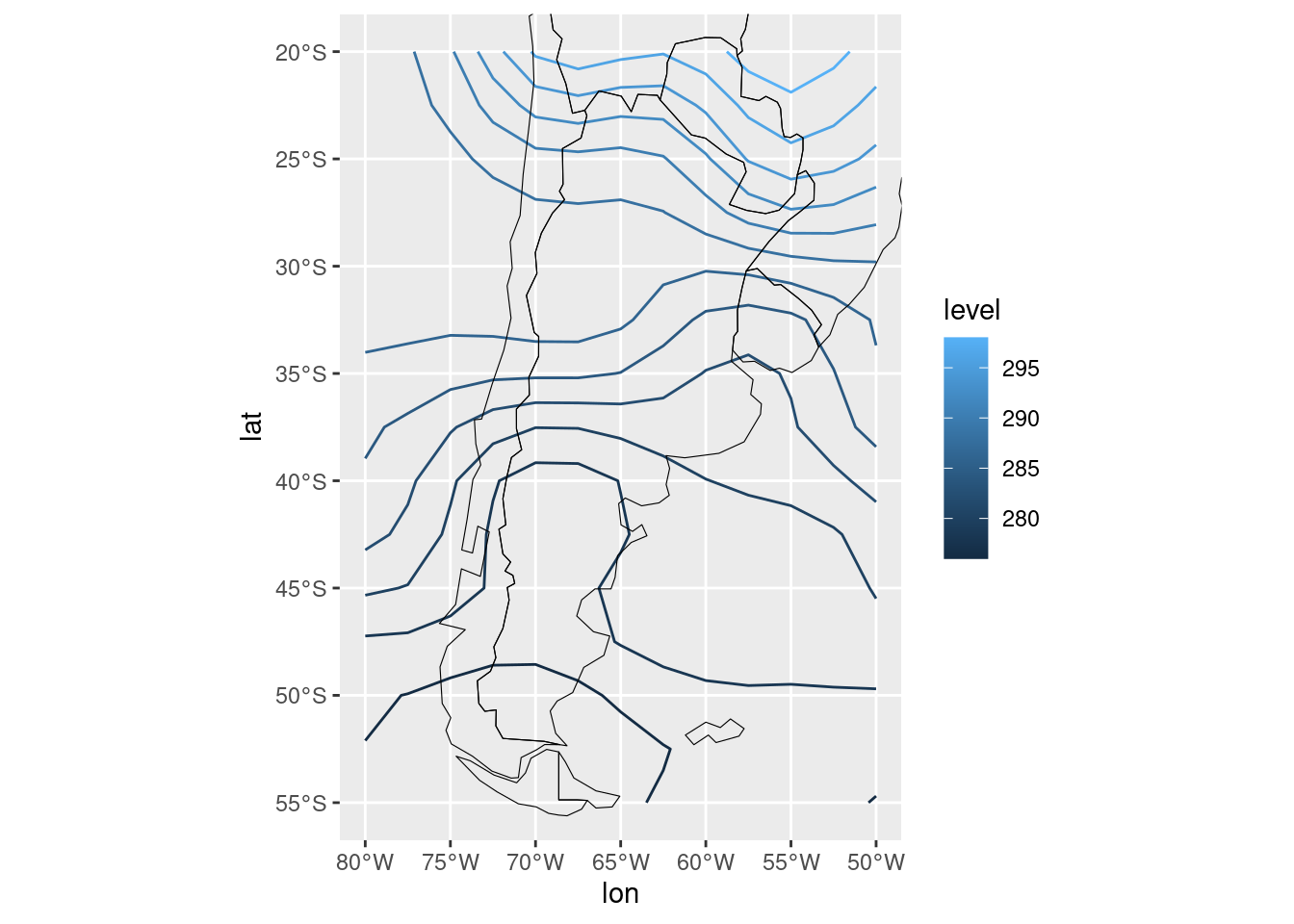
¿De dónde salió ese stat(level)? Algunos geoms que realizan transformaciones estadísticas computan variables nuevas que luego se pueden mapear a parámetros geométricos. “level” es una de esas variables computadas de geom_contour. Para decirle a ggplot que al level al que te referís es a la variable computada, se rodea a la variable con la función stat().

Una variedad de las líneas de contorno son las líneas “llenas”. Hasta hace poco, {ggplot2} no tenía una forma de graficar estos contornos llenos, así que está implementado en {metR} con la function geom_contour_fill(). Recientemente {ggplot2} implementó la función geom_contour_filled() pero a nosotros nos gusta más la versión de {metR} 😉

ggplot(temperatura, aes(lon, lat)) +
  metR::geom_contour_fill(aes(z = air)) +
  mi_mapa +
  coord_sf(ylim = c(-55, -20), xlim = c(-80, -50))

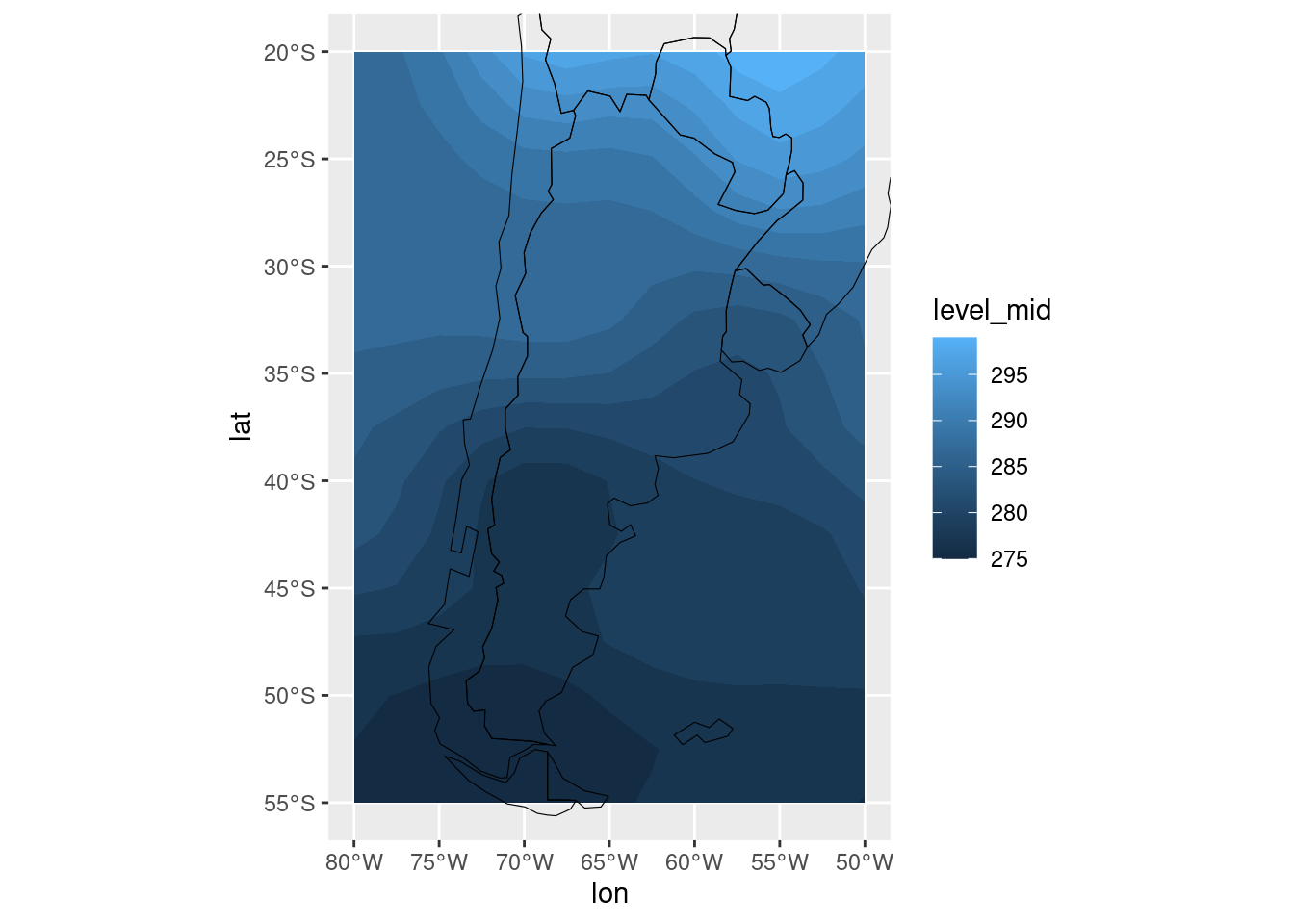
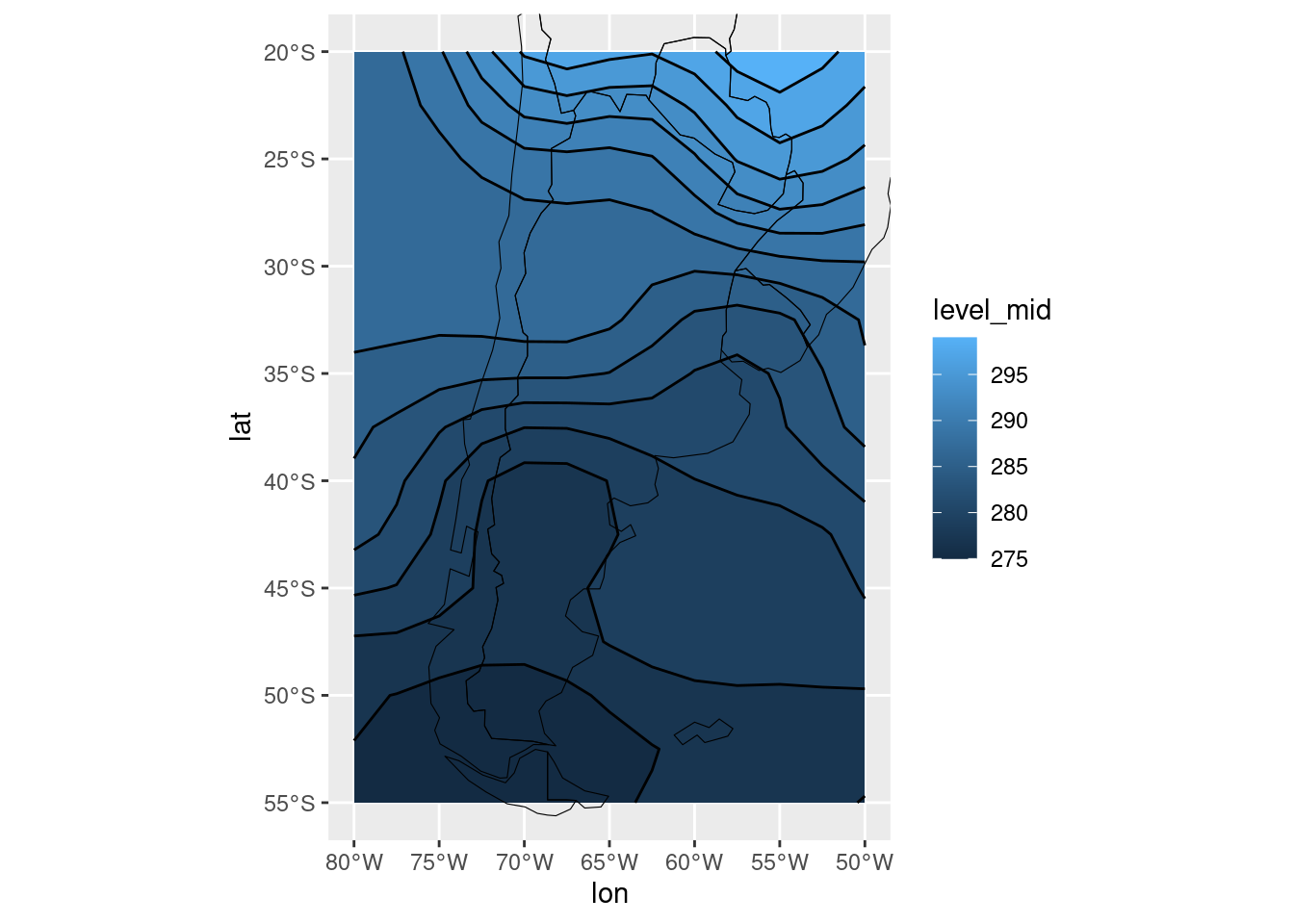
Por último, tranquilamente se pueden usar ambos geoms para resaltar los límites y

ggplot(temperatura, aes(lon, lat)) +
  metR::geom_contour_fill(aes(z = air)) +
  geom_contour(aes(z = air), color = "black") +
  mi_mapa +
  coord_sf(ylim = c(-55, -20), xlim = c(-80, -50))

Grillas irregulares

¿Qué pasa cuando en vez de observaciones organizadas en una bella grilla regular, tenés observaciones puntuales en lugares dispersos? Si te acordás de la sección de uniones, en la carpeta datos hay un archivo con datos de temperatura del servicio meteorológico y metadatos con sus ubicaciones. Esto define datos espaciales de temperatura.

# Para trabajar con menos datos, nos quedamos con la temperatura máxima media 
# de cada estación.
observaciones <- readr::read_csv("datos/observaciones_smn.csv") %>% 
  group_by(station) %>% 
  summarise(tmax_media = mean(tmax, na.rm = TRUE))

estaciones <- read_csv("datos/estaciones_smn.csv") 

observaciones <- left_join(observaciones, estaciones, by = c("station" = "nombre")) %>% 
  filter(provincia != "ANTARTIDA")

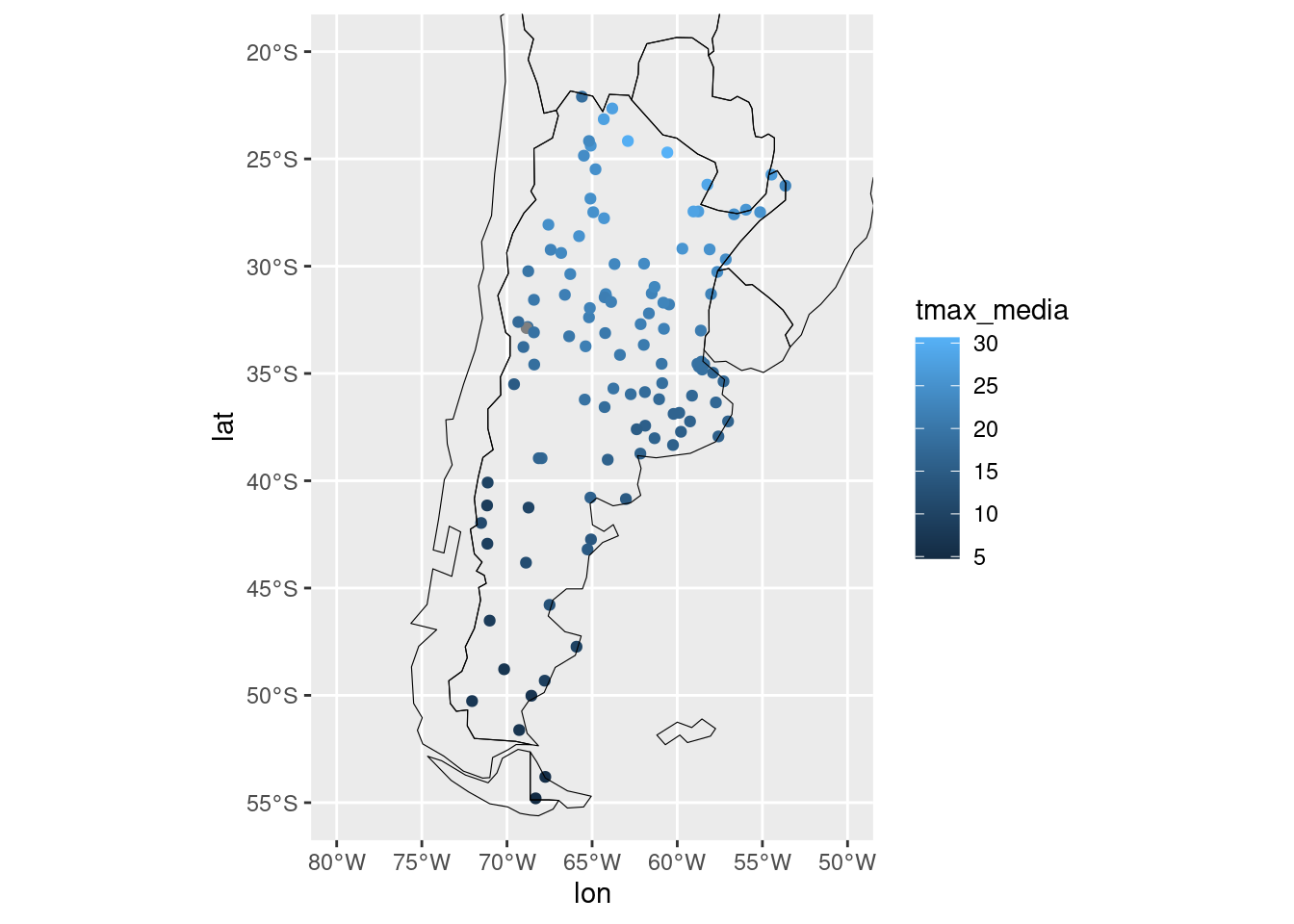
Lo primero que se puede hacer es graficar estos datos de estación con puntos, de la misma forma que para los datos regulares.

ggplot(observaciones, aes(lon, lat)) +
  geom_point(aes(color = tmax_media)) +
  mi_mapa +
  coord_sf(ylim = c(-55, -20), xlim = c(-80, -50))

Desafío

Graficá estos puntos usando geom_raster() y geom_contour(). ¿Cuál es el resultado?

Como estos datos no están en una grilla regular, geom_raster() y geom_contour() no los pueden graficar. Para usar contornos hay que interpolar a una grilla regular. Una forma de hacerlo es usando la técnica de kriging. Un paquete de R que la implementa es {kriging} en su función kriging

Si vas a la ayuda de kriging(), vas a ver que requiere un vector de coordenadas x, un vector de coordenadas y y un vector de valores observados. Estos son las columnas lon, lat y tmax_media de la tabla observaciones. Entonces el código sería:

observaciones_regular <- kriging::kriging(x = observaciones$lon, 
                                          y = observaciones$lat,
                                          response = observaciones$tmax_media)

## Error in onedim(response, n): NA/NaN/Inf in foreign function call (arg 1)

Este error indica que hay NAs, y kriging() no funciona si hay valores faltantes. Lo que hay que hacer es omitirlos. La función na.omit() elimina filas donde algún valor sea NA.

na.omit(observaciones)

## # A tibble: 115 × 6
##    station                   tmax_media provincia         lon   lat altua
##    <chr>                          <dbl> <chr>           <dbl> <dbl> <dbl>
##  1 AEROPARQUE AERO                17.4  CAPITAL FEDERAL -58.4 -34.6     6
##  2 AZUL AERO                      16.4  BUENOS AIRES    -59.9 -36.8   147
##  3 BAHIA BLANCA AERO              16.0  BUENOS AIRES    -62.2 -38.7    83
##  4 BARILOCHE AERO                  8.63 RIO NEGRO       -71.2 -41.2   835
##  5 BENITO JUAREZ AERO             15.6  BUENOS AIRES    -59.8 -37.7   207
##  6 BERNARDO DE IRIGOYEN AERO      22.4  MISIONES        -53.6 -26.2   815
##  7 BOLIVAR AERO                   17.4  BUENOS AIRES    -61.1 -36.2    94
##  8 BUENOS AIRES OBSERVATORIO      19.0  CAPITAL FEDERAL -58.5 -34.6    25
##  9 CAMPO DE MAYO AERO             18.8  BUENOS AIRES    -58.7 -34.5    26
## 10 CATAMARCA AERO                 25.1  CATAMARCA       -65.8 -28.6   464
## # … with 105 more rows

Para no escribir na.omit(observaciones) tres veces dentro de la llamada a krigin() se puede usar la función with(). Esta función no es de {dplyr} pero funciona parecido a summarise()/mutate() en que toma como primer argumento una tabla y luego el código que pongamos se entiende que hace referencia a las columnas de esa tabla.

Entonces, poniendo todo eso junto en una cadena:

observaciones_regular <- observaciones %>% 
  na.omit() %>% 
  with(kriging::kriging(lon, lat, response = tmax_media))

Desafío

¿Qué es lo que devolvió la función kriging()? Podés mirar la documentación de la función (en la sección “Value”) o usando glimpse(observaciones_regular).

observaciones_regular es una lista con muchos elementos:

glimpse(observaciones_regular)

## List of 7
##  $ model        : chr "spherical"
##  $ nugget       : num -4.4
##  $ range        : num 11.9
##  $ sill         : num 26.9
##  $ pixel        : num 0.33
##  $ map          :'data.frame':   5544 obs. of  3 variables:
##   ..$ x   : num [1:5544] -72 -72 -72 -72 -72 ...
##   ..$ y   : num [1:5544] -54.8 -54.5 -54.1 -53.8 -53.5 ...
##   ..$ pred: num [1:5544] 8.94 8.74 8.55 8.38 8.24 ...
##  $ semivariogram:'data.frame':   10 obs. of  2 variables:
##   ..$ distance    : num [1:10] 0.685 1.943 3.143 4.41 5.628 ...
##   ..$ semivariance: num [1:10] 0.555 2.139 3.295 5.659 8.877 ...
##  - attr(*, "class")= chr "kriging"

La mayoría de los elementos brindan información detallad sobre los parámetros usados y computados para realizar la interpolación. El elemento útil es el que se llama map, que tiene los datos interpolados. ¿Qué es lo que tiene map?

glimpse(observaciones_regular$map)

## Rows: 5,544
## Columns: 3
## $ x    <dbl> -72.05, -72.05, -72.05, -72.05, -72.05, -72.05, -72.05, -72.05, -…
## $ y    <dbl> -54.80000, -54.46970, -54.13939, -53.80909, -53.47879, -53.14848,…
## $ pred <dbl> 8.938263, 8.740744, 8.554452, 8.379149, 8.240792, 8.154581, 8.111…

Es una tabla con columnas, “x”, “y” y “pred”, que representan las coordenadas horizontales y los valores interpolados. Estos nombres no son muy descriptivos; se pueden cambiar con rename. Entonces este código extrae el elemento map de la lista observaciones_regular, le cambia el nombre a las variables y asigna el resultado a observaciones_regular

observaciones_regular <- observaciones_regular$map %>% 
  rename(lon = x, lat = y, tmax_media = pred)

Y esto, como es una grilla regular, se puede graficar con cualquiera de las técnicas anteriores. Dado que esto es una interpolación, es buena costumbre, además, indicar con puntos las coordenadas de las observaciones usadas para realizarla.

ggplot(observaciones_regular, aes(lon, lat)) +
  geom_contour_fill(aes(z = tmax_media)) +
  geom_point(data = observaciones, size = 0.2) +
  mi_mapa +
  coord_sf(ylim = c(-55, -20), xlim = c(-80, -50))

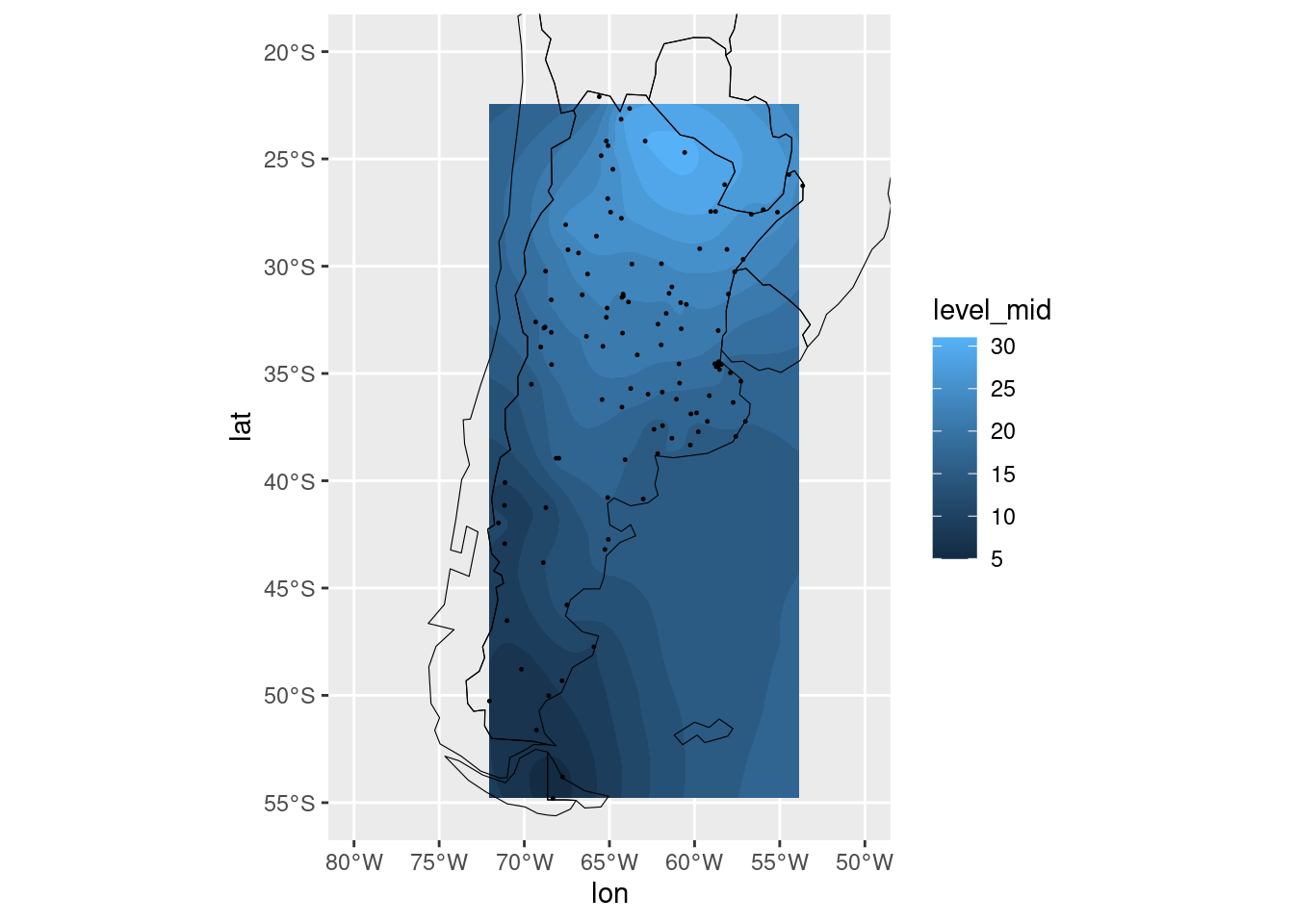
Este mapa se puede mejorar. En particular, la interpolación en el Mar Argentino, a miles de kilómetros de cualquier observación, no tiene ningún sentido. Para controlar el dominio en el cual se realiza la interpolación hay que usar el argumento polygons de kriging(). Ahí, hay que poner puntos en x e y que definan el polígono dentro del cual se va a hacer la interpolación. ¿De dónde sacás un polígono con el contorno de Argentina? 🤔. ¡Lo estás mirando! Es nuestro mapa.

La función fortify() de {ggplot2} genera polígonos a partir de la salida de {rnaturalearth}. De esos polígonos hay que seleccionar únicamente las coordenadas de longitud y latitud, y al mismo tiempo, renombrarlas como x e y para que kriging() las entienda. Finalmente, hay que meter todo eso en una lista.

poligonos_arg <- rnaturalearth::ne_countries(country = "argentina") %>% 
  fortify() %>% 
  select(x = long, y = lat) %>% 
  list()

Ahora, hay que repetir todo lo anterior, pero usando con polygons = poligonos_arg.

observaciones_regular <- observaciones %>% 
  na.omit() %>% 
  with(kriging::kriging(lon, lat, response = tmax_media, polygons = poligonos_arg)) 

observaciones_regular <- observaciones_regular$map %>% 
  rename(lon = x, lat = y, tmax_media = pred)

ggplot(observaciones_regular, aes(lon, lat)) +
  geom_contour_fill(aes(z = tmax_media)) +
  geom_point(data = observaciones, size = 0.2) +
  mi_mapa +
  coord_sf(ylim = c(-55, -20), xlim = c(-80, -50))

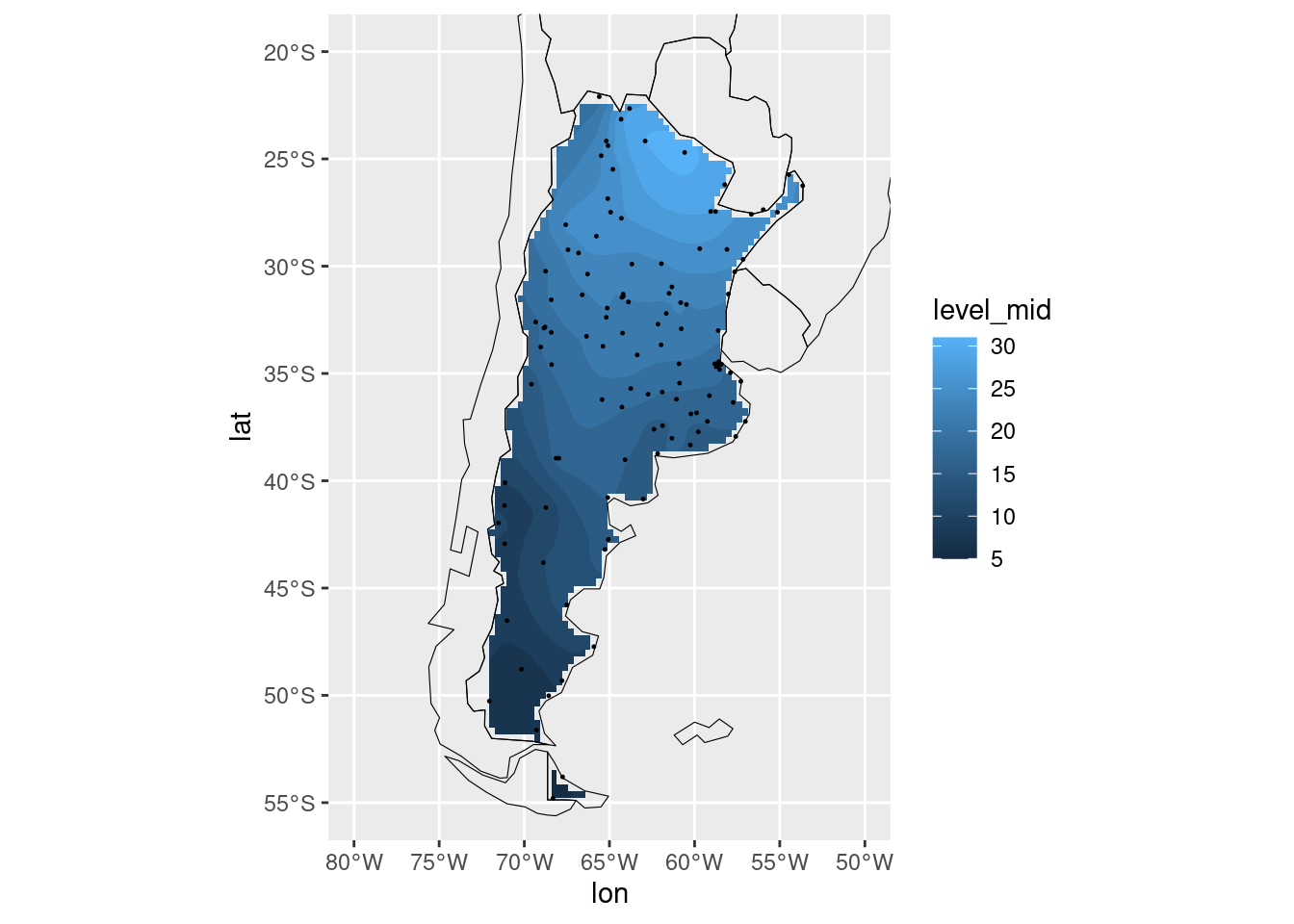
Desafío

La interpolación de este gráfico queda fea en los bordes porque tiene poca resolución. ¿Qué hay que cambiar en la llamada a kriging() para incrementarla? Fijate en la documentación de la función.

Este gráfico tiene lo básico, pero se le puede poner un poco de amor para que quede mejor. Se le puede agregar líneas de contorno en negro para resaltar los contornos, cambiar la escala de colores para que evoque más la idea de “temperatura máxima”, agregar etiquetas a los contornos y modificar el texto de los ejes y las escalas. Haciendo todo eso, podemos llegar a algo como esto.

ggplot(observaciones_regular, aes(lon, lat)) +
  geom_contour_fill(aes(z = tmax_media)) +
  geom_contour2(aes(z = tmax_media), size = 0.2) +
  geom_text_contour(aes(z = tmax_media), skip = 1,
                    rotate = FALSE, size = 3.5,
                    stroke = 0.1, color ="white", stroke.color = "black") +
  geom_point(data = observaciones, size = 0.2) +
  mi_mapa +
  scale_fill_distiller(palette = "YlOrRd", direction = 1) +
  coord_sf(ylim = c(-55, -20), xlim = c(-80, -50)) +
  labs(fill = "Temperatura (ºC)", 
       x = NULL,
       y = NULL)  +
  theme_minimal()

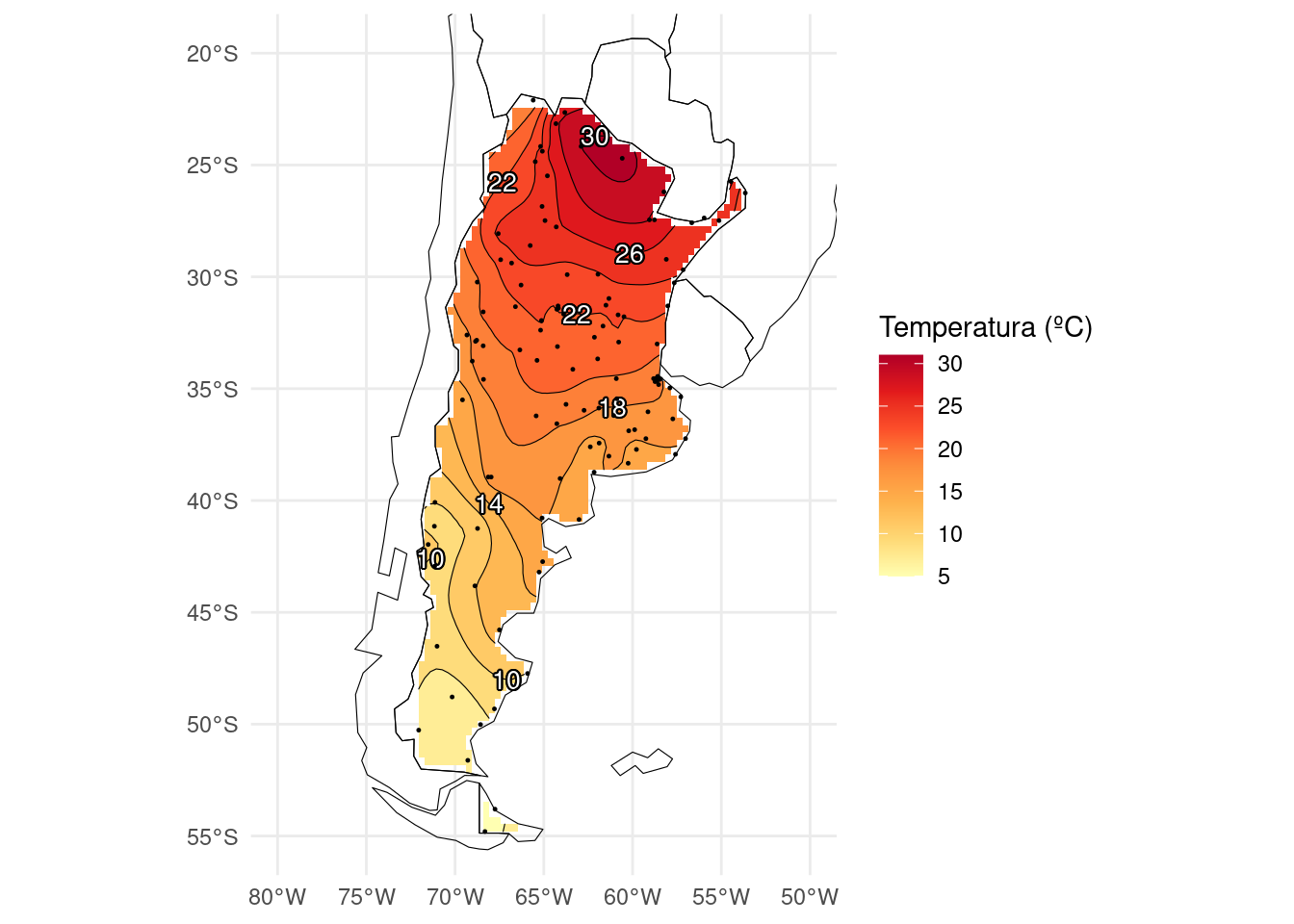
Vas av er un poco más sobre la apariencia de los gráficos en la siguiente sección.