Calculos
Haciendo cálculos
Una de las grandes ventajas de tener los datos organizados en un data.frame tidy es que es posible aplicar todas las técnicas de análisis de datos tradicionales a estos datos grillados.
# Cargo los paquetes necesarios
library(magrittr)
library(ggplot2)
library(dplyr)
library(data.table)
library(metR)
# función para generar un mapa
mapa <- function(fill = "white", colour = NA) {
geom_polygon(data = map_data("world2"), aes(long, lat, group = group),
fill = fill, colour = colour, inherit.aes = FALSE, size = 0.2)
}
# Leo los datos
sst <- ReadNetCDF("datos/temperatura_mar.nc", vars = "sst")Por ejemplo, ¿cómo calcularías un el campo medio de temperatura de la superficie del mar (SST)? Esencialmente es calcular el promedio de sst para cada longitud y latitud, una operación que se traduce de forma directa a operaciones en grupos.
data.table
sst %>%
.[, .(sst = mean(sst)), by = .(longitude, latitude)] %>%
ggplot(aes(longitude, latitude)) +
geom_contour_fill(aes(z = sst), na.fill = TRUE) +
mapa()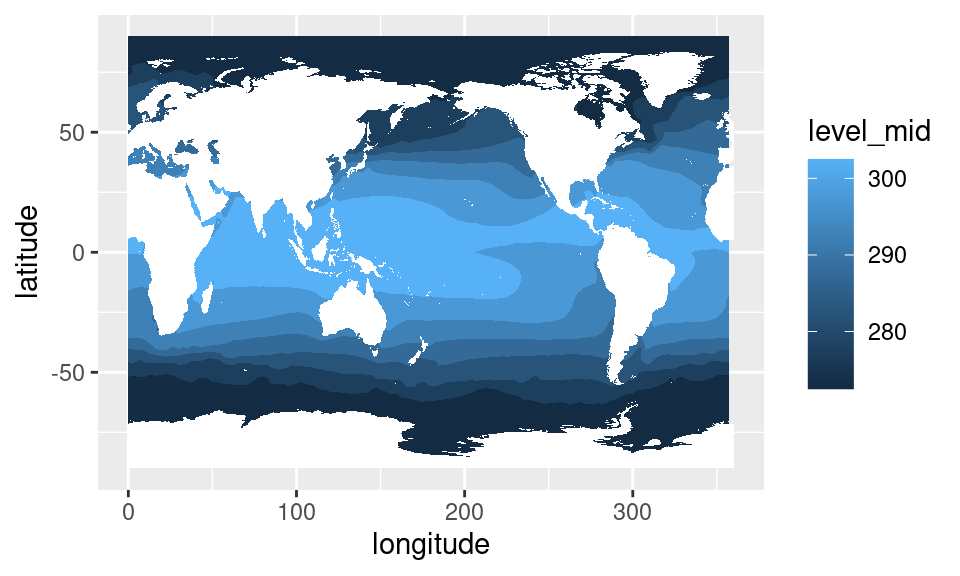
dplyr
sst %>%
group_by(longitude, latitude) %>%
summarise(sst = mean(sst)) %>%
ungroup() %>%
ggplot(aes(longitude, latitude)) +
geom_contour_fill(aes(z = sst), na.fill = TRUE) +
mapa() 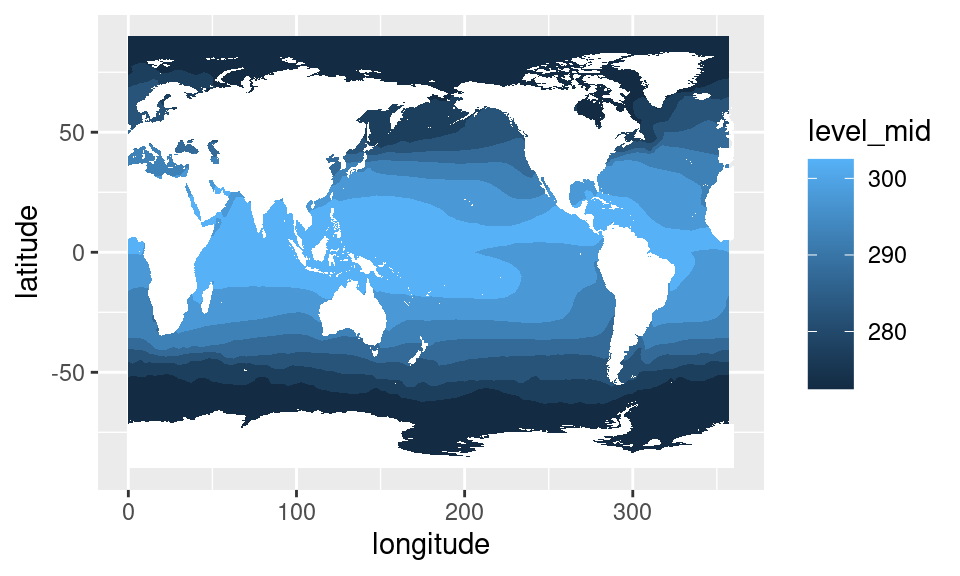
Veamos ahora series temporales te SST en distintos puntos, para tener una idea de algunas características de su variabilidad.
Definamos tres puntos que representan zonas muy disímiles del planeta:
puntos <- tibble::tribble(~longitude, ~latitude,
180 , 0,
170 , 50,
280 , -60) %>%
as.data.table()ggplot(puntos, aes(longitude, latitude)) +
geom_point() +
mapa()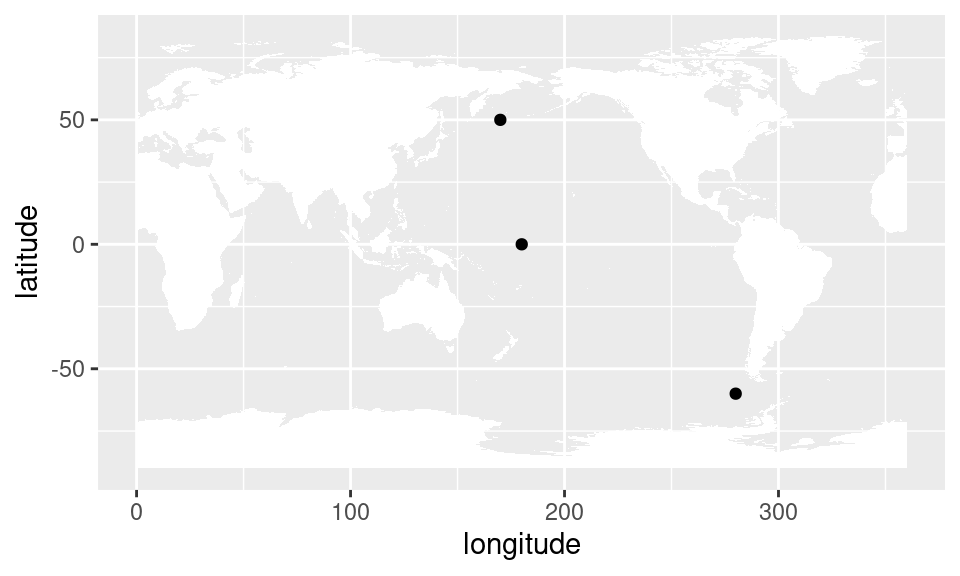
Para filtrar los datos de SST correspondientes a esos puntos, se puede hacer un join.
data.table
sst %>%
.[puntos, on = .NATURAL] %>%
ggplot(aes(time, sst)) +
geom_line()+
facet_wrap(~ longitude + latitude, scales = "free_y",
labeller = label_both, ncol = 1)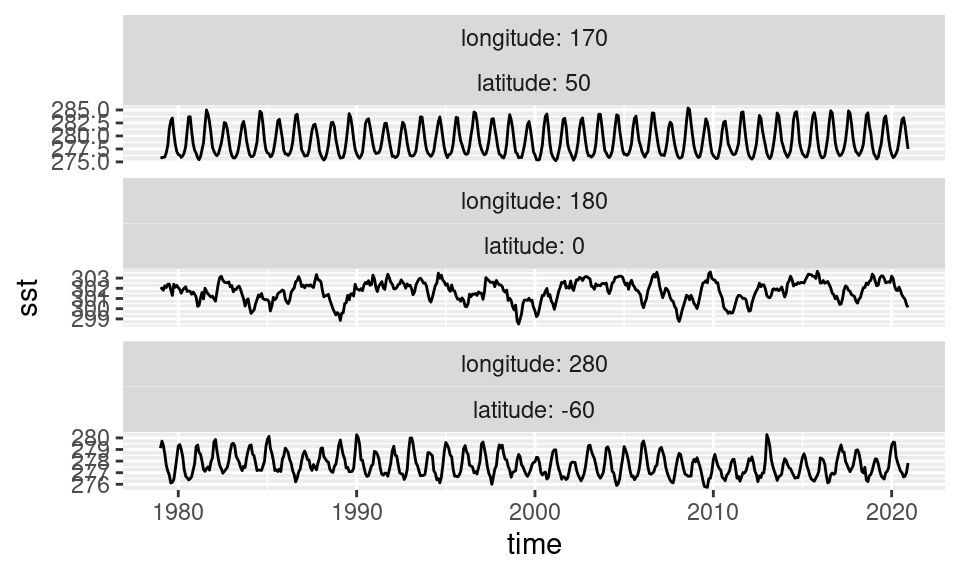
dplyr
sst %>%
right_join(puntos) %>%
ggplot(aes(time, sst)) +
geom_line()+
facet_wrap(~ longitude + latitude, scales = "free_y",
labeller = label_both, ncol = 1)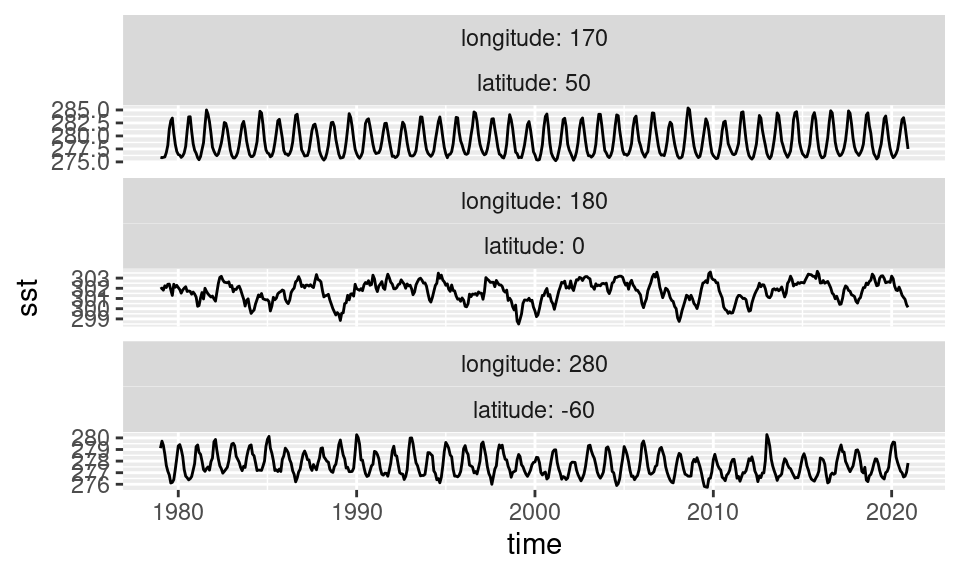
Se puede ver que las región tropical tiene una variabilidad de relativa baja frecuencia y sin un ciclo anual pronunciado. Por otro lado, en los puntos extratropicales la variabilidad más fuerte es el ciclo anual, que naturalmente se invierte entre el hemisferio norte y el hemisferio sur.
Pero el ciclo anual no es interesante, es una variabilidad casi constante, predecible. Lo que es interesante es lo impredecible, lo que se aleja del ciclo anual. Para esto se calculan las anomalías: el alejamiento de los datos con respecto a el ciclo anual promedio.
Para calcular anomalías, hay que calcular el valor del dato menos el valor promedio del dato, para cada mes, y cada latitud y longitud. Nuevamente esto se traduce durectamente en operaciones sobre grupos.
data.table
sst[, sst_a := sst - mean(sst), by = .(longitude, latitude, month(time))] dplyr
sst <- sst %>%
group_by(longitude, latitude, mes = month(time)) %>%
mutate(sst_a = sst - mean(sst)) %>%
ungroup() %>%
select(-mes)Entonces ahora podemos ver a las anomalías. Por definición, las anomalías tienen media cero y lo interesante es ver cuánto se alejan de ese promedio, lo cual hacer que una escala divergente sea la elección natural para visualizarlas.
sst %>%
.[time == unique(time)[229]] %>% # elijo un mes en particular
ggplot(aes(longitude, latitude)) +
geom_contour_fill(aes(z = sst_a), na.fill = TRUE) +
mapa() +
scale_fill_divergent()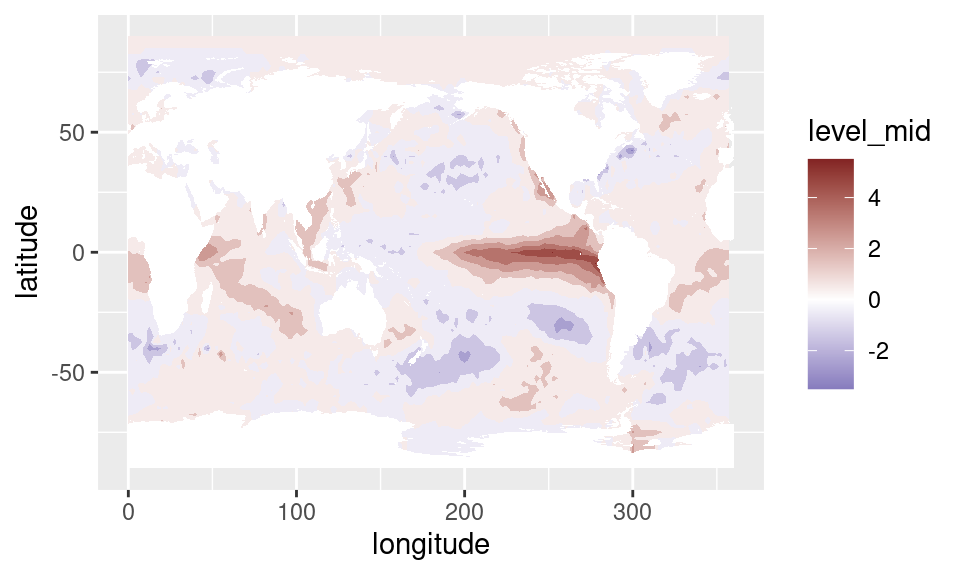
EOF
Algunos métodos con datos grillados se presetan de forma más natural a la oganización de datos grillados en forma de matriz. Análisis de Componentes Principales (también llamado Empirical Orthogonal Functions en ciencias de la atmósfera) es uno de ellos.
metR tiene la función EOF() que aplica componentes principales a los datos. Su primer argumento es una fórmula que define la estructura de la matriz de entrada a partir de los datos.
Esta fórmula tiene la forma general:
variable ~ x + y | a + bLa idea es leer esto como
“variable en función de la combinación de x e y en las filas y la combinación de a y b en las columnas”
Entonces, vamos a calcular los primeros dos EOFs del campo de anomalías de SST.
data.table
eofs <- sst %>%
.[!is.na(sst_a)] %>%
.[, sst_a := sst_a*sqrt(cos(latitude*pi/180))] %>%
EOF(sst_a ~ longitude + latitude | time, n = 1:2, data = .)dplyr
eofs <- sst %>%
filter(!is.na(sst_a)) %>%
mutate(sst_a = sst_a*sqrt(cos(latitude*pi/180))) %>%
EOF(sst_a ~ longitude + latitude | time, n = 1:2, data = .)EOF() devuelve una lista de data.tables con la parte izqueirda, derecha y la varianza explicada por cada componente.
str(eofs)## List of 3
## $ left :Classes 'data.table' and 'data.frame': 13832 obs. of 4 variables:
## ..$ longitude: num [1:13832] 0 2.5 5 7.5 10 12.5 15 17.5 20 22.5 ...
## ..$ latitude : num [1:13832] 90 90 90 90 90 90 90 90 90 90 ...
## ..$ PC : Ord.factor w/ 2 levels "PC1"<"PC2": 1 1 1 1 1 1 1 1 1 1 ...
## ..$ sst_a : num [1:13832] 7.33e-15 7.33e-15 7.33e-15 7.33e-15 7.33e-15 ...
## ..- attr(*, ".internal.selfref")=<externalptr>
## $ right:Classes 'data.table' and 'data.frame': 1008 obs. of 3 variables:
## ..$ time : POSIXct[1:1008], format: "1979-01-01" "1979-02-01" ...
## ..$ PC : Ord.factor w/ 2 levels "PC1"<"PC2": 1 1 1 1 1 1 1 1 1 1 ...
## ..$ sst_a: num [1:1008] -0.0186 -0.00745 -0.00186 -0.01872 -0.02797 ...
## ..- attr(*, ".internal.selfref")=<externalptr>
## $ sdev :Classes 'data.table' and 'data.frame': 2 obs. of 3 variables:
## ..$ PC: Ord.factor w/ 2 levels "PC1"<"PC2": 1 2
## ..$ sd: num [1:2] 358 325
## ..$ r2: num [1:2] 0.138 0.114
## ..- attr(*, ".internal.selfref")=<externalptr>
## - attr(*, "call")= language EOF(formula = sst_a ~ longitude + latitude | time, n = 1:2, data = .)
## - attr(*, "class")= chr [1:2] "eof" "list"
## - attr(*, "suffix")= chr "PC"
## - attr(*, "value.var")= chr "sst_a"
## - attr(*, "engine")=function (A, nv, nu)Si queremos ver la parte espacial, extraemos la parte izquierda:
eofs$left %>%
ggplot(aes(longitude, latitude)) +
geom_contour_fill(aes(z = sst_a)) +
mapa() +
scale_fill_divergent() +
facet_wrap(~PC, ncol = 1)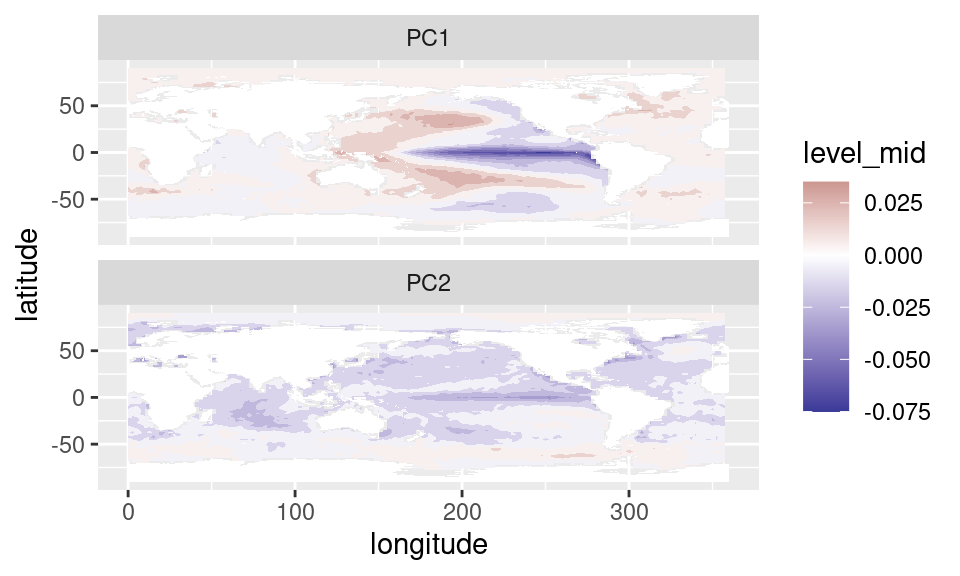
Es primera componente principal nos indica que la mayor parte de la variabildiad de SST está asociada a cambios en la temperatura del Pacífico ecuatorial. Esto se conoce como la oscilación de El Niño.
Una forma de calcular un índice de esta oscilación que no requiere calculos “raros” como EOF es con el índice ENSO34, que se define como las anomalías de temperatura promedio entre 5ºS y 5ºN en la región entre 170ºO y 120ºO.
Podemos calcular este índice con nuestros datos filtrando primero los datos que están en esa caja y luego calculando el promedio para cada tiempo. Nuevamente, estas son operaciones básicas del análisis de datos tidy.
data.table
enso <- sst %>%
.[abs(latitude) < 5 & ConvertLongitude(longitude) %between% c(-170, -120)] %>%
.[, .(enso34 = mean(sst_a)), by = time]dplyr
enso <- sst %>%
filter(abs(latitude) < 5 & between(ConvertLongitude(longitude), -170, -120)) %>%
group_by(time) %>%
summarise(enso34 = mean(sst_a)) %>%
ungroup()El resultado:
ggplot(enso, aes(time, enso34)) +
geom_line() +
geom_hline(yintercept = c(-0.5, 0.5))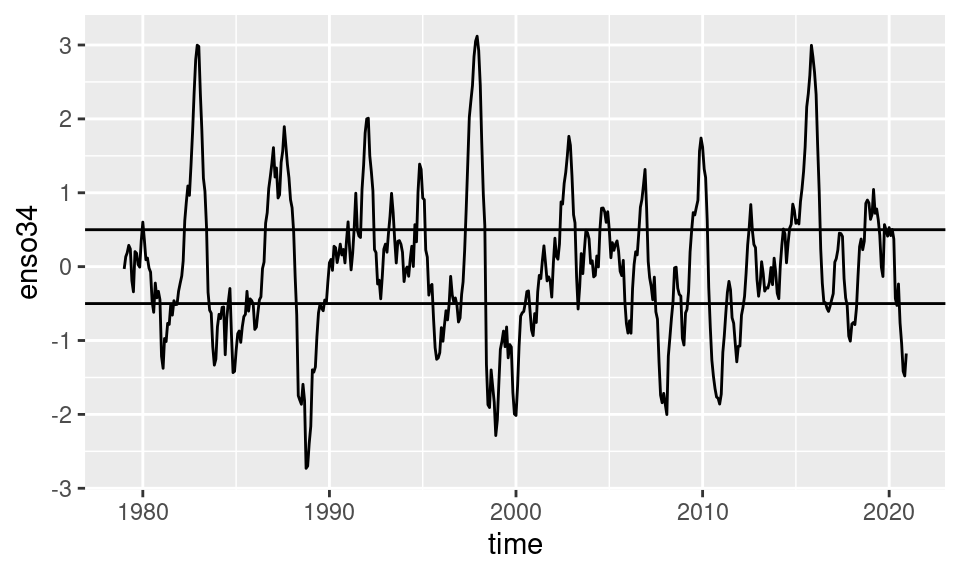
Las líneas horizontales marcan los valores de +0.5 y -0.5 que se usan tradicionalmente para definir eventos de ENSO positivos y negativos respetivamente.
Regresiones y correlaciones
Para asegurarnos de que este índice realmetne representa lo que creemos que representa, podemos calcular la regresión de la SST en cada punto con este índice. Para eso primero hay que unir los datos de SST con el índice que calculamos y luego calcular la regresión en cada punto.
Un problema acá es que lm() es muy lento principalmente porque se toma mucho tiempo tratando de entender la fórmula que es el primer argumento. Para acelerar las cosas, metR tiene la función FitLm() que sirve para calcular los coeficientes de regresiones lineales mucho más rápido.
data.table
sst %>%
.[enso, on = "time"] %>%
.[, FitLm(sst_a, enso34), by = .(longitude, latitude)] %>%
.[term != "(Intercept)"] %>%
ggplot(aes(longitude, latitude)) +
geom_contour_fill(aes(z = estimate), na.fill = 0) +
mapa() +
scale_fill_divergent()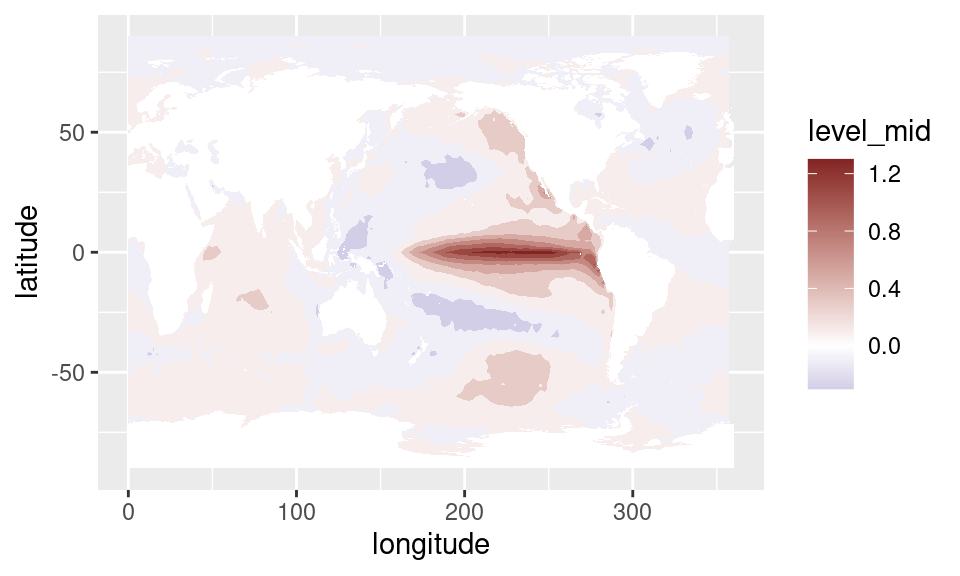
dplyr
sst %>%
right_join(enso, by = "time") %>%
group_by(latitude, longitude) %>%
summarise(as.data.frame(FitLm(sst_a, enso34))) %>%
ungroup() %>%
filter(term != "(Intercept)") %>%
ggplot(aes(longitude, latitude)) +
geom_contour_fill(aes(z = estimate), na.fill = 0) +
mapa() +
scale_fill_divergent()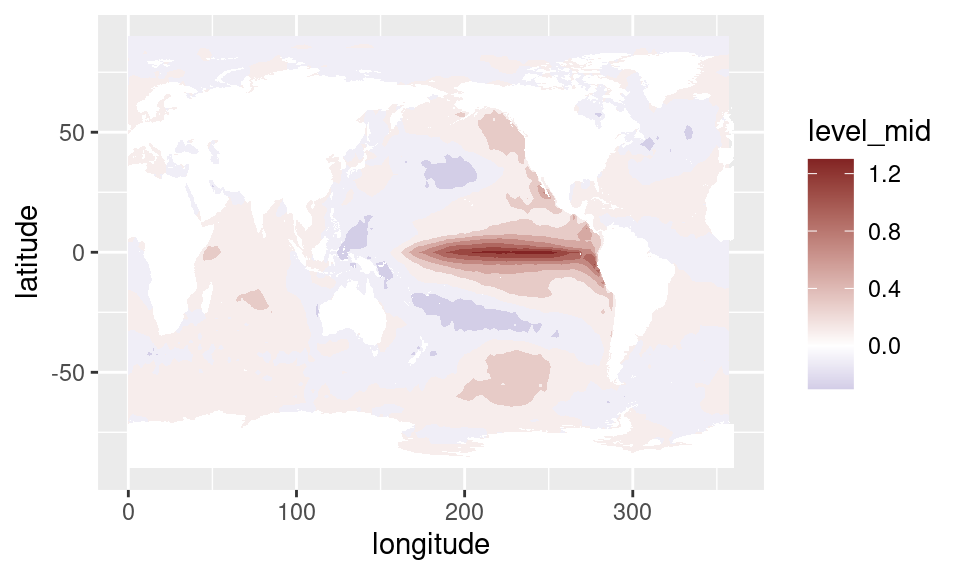
Esto se ve bien. Ahora podemos ver si hay relación entre este índice y otras variables climáticas.
Leamos los datos de presión a nivel del mar y precipitación total.
datos <- ReadNetCDF("datos/temperatura_mar.nc",
vars = c("msl", pp = "tp"))data.table
correlacion <- datos %>%
melt(id.vars = c("time", "longitude", "latitude")) %>%
.[, value := value - mean(value), by = .(longitude, latitude, variable, month(time))] %>%
.[enso, on = "time"] %>%
.[, .(correlacion = cor(value, enso34)), by = .(latitude, longitude, variable)]dplyr
correlacion <- datos %>%
tidyr::pivot_longer(cols = c(msl, pp), names_to = "variable") %>%
group_by(longitude, latitude, variable, month(time)) %>%
mutate(value = value - mean(value)) %>%
left_join(enso, by = "time") %>%
group_by(latitude, longitude, variable) %>%
summarise(correlacion = cor(value, enso34)) %>%
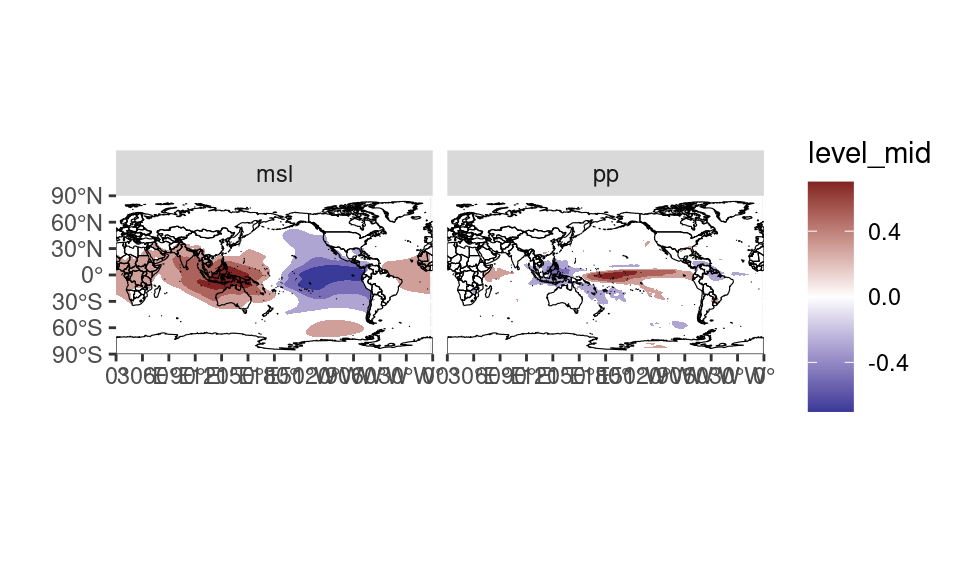
ungroup()correlacion %>%
ggplot(aes(longitude, latitude)) +
geom_contour_fill(aes(z = correlacion), breaks = AnchorBreaks(exclude = 0)) +
scale_fill_divergent() +
mapa(fill = NA, colour = "black") +
scale_x_longitude() +
scale_y_latitude() +
coord_quickmap() +
facet_wrap(~variable, ncol = 2)