Metamerismo estadístico
In English: Statistical metamerismResumen
El paquete metamer implementa en R el algoritmo descripto por Matejka and Fitzmaurice (2017) para generar sets de datos distintos entre sí pero con estadísticos idénticos. Además, propongo el nombre “metámeros” para estos grupos de datos en analogía con el concepto proveniente de colorimetría.
Metámeros en la visión
Esto no es un prisma separando la luz blanca en las longitudes de onda que la componen. Es una imagen de un prisma separando la luz blanca en las longitudes de onda que la componen.

Fig. 1: C’est ne pas un prisme.
Esta observación magrittiana no es trivial. El monitor que está mostrando la imagen sólo tiene tres LEDs que emiten luz en sólo tres longitudes de onda (más o menos). ¿Cómo hace para reproducir todo el espectro de la luz blanca? La respuesta es que no lo hace. Para cada color de ese arcoíris, el monitor está emitiendo una mezcla de longitudes de onda roja, verde y azul que nuestro sistema visual interpreta como el mismo color que esa longitud de onda específica.
Cómo sucede todo eso es complicadísimo y va más allá de lo que pueda explicar en este artículo (pero sí recomiendo leer esta excelente nota sobre el tema) pero el núcleo de la cuestión es que nuestros ojos tienen sólo tres tipos de receptores (conos) que responden a longitudes de onda cortas (S), medias (M) y largas (L). Por lo tanto, cualquier distribución de longitudes de onda que llegue a nuestros ojos, sin importar cuán complicada sea es reducida a únicamente tres números: la excitación de los receptores S, M y L. Y cualquier distribución de longitudes de onda que excite nuestros receptores en la misma proporción va a ser percibido como el mismo color. En colorimetría, esto se conoce como metamerismo (Hunt 2004). El amarillo monocromático que se ve en un prisma se percibe igual que el amarillo producido por el monitor aunque no tenga ni remotamente el mismo espectro. Son metámeros.
La creación de pares metaméricos es la base de la reproducción del color en monitores, impresiones y cuadros, pero también tiene su lado oscuro. Dos pigmentos pueden ser pares metaméricos bajo ciertas condiciones de iluminación pero tener colores muy distintos en otras. Esto puede ser un problema, por ejemplo, al comprar ropa en un negocio con iluminación artificial y luego usarla bajo la luz del Sol.
Metámeros en la estadística
Ahora pensemos en el famoso cuarteto de Anscombe
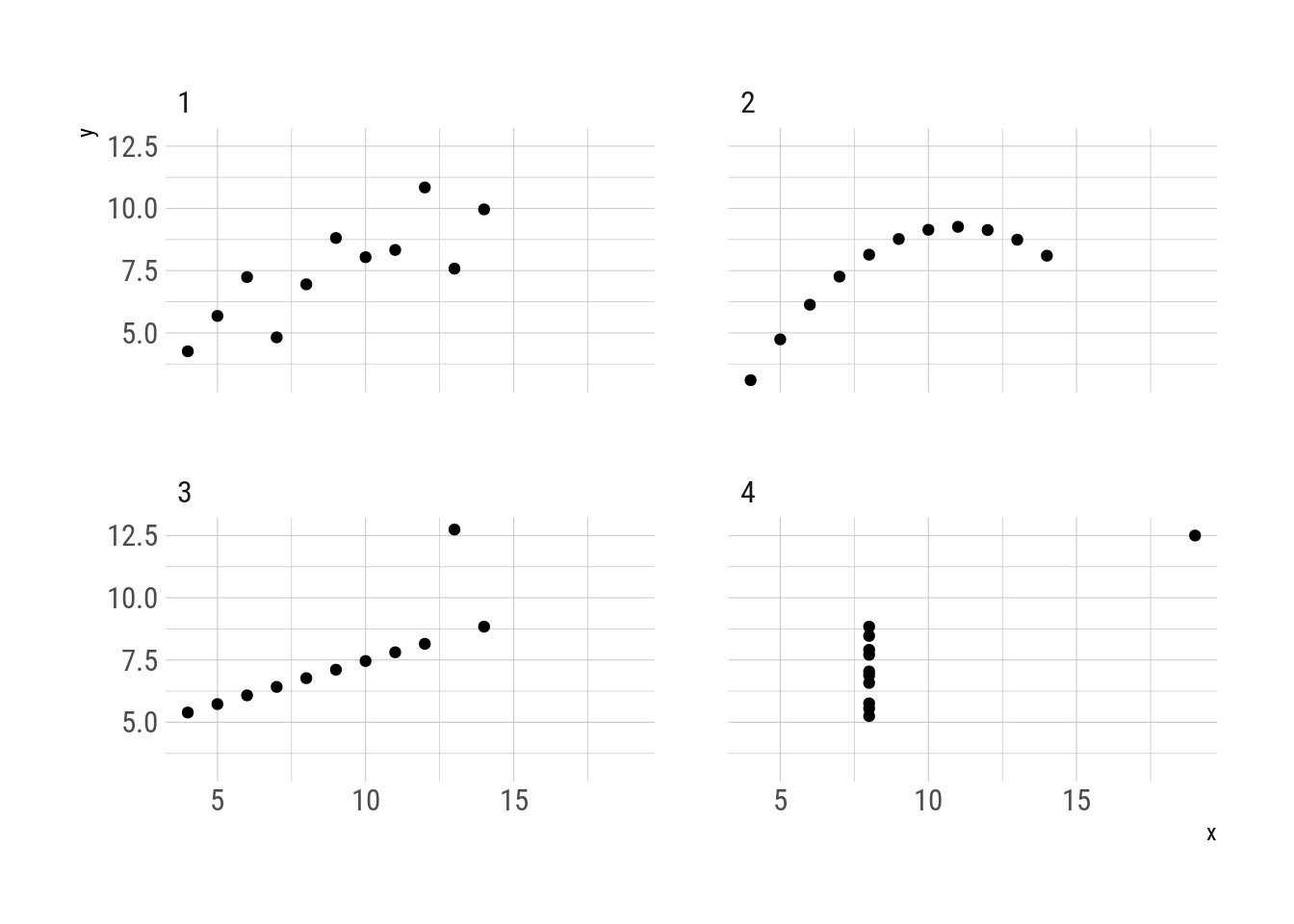
Fig. 2: Cuarteto de Anscombe
A pesar de ser cuatro sets de datos muy distintos, los miembros del cuarteto comparten el promedio y desvío estándar de cada variable, así como la correlación entre ambas (Anscombe 1973). Vistos a través de esta transformación estadística, los cuatro sets de datos se ven iguales aún cuando no son ni remotamente similares. Son metámeros.
Al igual que los pares metaméricos de colores, los metámeros estadísticos muestran sus diferencias cuando se los ve con otra “iluminación.” En este caso, un gráfico.
El concepto de “datos con estadísticos idénticos pero gráficos distintos” todavía tiene relevancia, con varias publicaciones describiendo distintos métodos para crearlos (p.e. Chatterjee and Firat 2007; Govindaraju and Haslett 2008; Haslett and Govindaraju 2009; Matejka and Fitzmaurice 2017) pero, que yo sepa, nunca fue nombrado. En analogía al metamerismo del color, en este artículo voy a llamar “metámeros” a cualquier conjunto de sets de datos que se comporta de forma idéntica bajo una determinada transformación estadística.
El paquete metamer implementa el algoritmo de Matejka and Fitzmaurice (2017) para generar metámeros. La función principal, metamerize(), permite generar metámeros a partir de un data set inicial y una función a preservar. Opcionalmente, se puede establecer una función que deben minimizar los metámeros sucesivos.
Primero, la función delayed_with() sirve para definir la serie de transformaciones estadísticas que deben ser preservadas. Los cuatro elementos del cuarteto de anscombe preservan estas propiedades con hasta tres cifras significativas (salvo por la correlación entre x e y en el cuarto cuarteto).
library(metamer)
summ_fun <- delayed_with(mean_x = mean(x),
mean_y = mean(y),
sd_x = sd(x),
sd_y = sd(y),
cor_xy = cor(x, y))
summ_names <- c("$\\overline{x}$", "$\\overline{y}$",
"$S_x$", "$S_y$", "$r(x, y)$")
anscombe[, as.list(signif(summ_fun(.SD), 3)), by = quartet] %>%
knitr::kable(col.names = c("Cuarteto", summ_names),
escape = FALSE,
caption = "Propiedades estadísticas del cuarteto de Anscombe")| Cuarteto | \(\overline{x}\) | \(\overline{y}\) | \(S_x\) | \(S_y\) | \(r(x, y)\) |
|---|---|---|---|---|---|
| 1 | 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 2 | 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 3 | 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 4 | 9 | 7.5 | 3.32 | 2.03 | 0.817 |
Para encontrar metámeros “entre” el primero y el segundo cuarteto, se puede empezar por el primero y generar metámeros que minimicen la distancia media al segundo. La función mean_dist_to() sirve para este caso.
# Extraigo el segundo cuarteto y eliminto la columna `quartet`
start_data <- subset(anscombe, quartet == 1)
start_data$quartet <- NULL
# Exraigo el tercer cuarteto y eliminto la columna `quartet`
target <- subset(anscombe, quartet == 2)
target$quartet <- NULL
set.seed(42) # para resultados reproducibles
metamers <- metamerize(start_data,
preserve = summ_fun,
minimize = mean_dist_to(target),
signif = 3,
change = "y",
perturbation = 0.008,
N = 30000)
print(metamers)## List of 4690 metamersEl proceso genera 4689 metámeros además de los datos originales. Seleccionando sólo 10 usando trim() y aplicando summ_fun() a cada uno se confirma que tienen las mismas propiedades con 3 cifras significativas.
metamers %>%
trim(10) %>%
lapply(summ_fun) %>%
lapply(signif, digits = 3) %>%
do.call(rbind, .) %>%
knitr::kable(col.names = c(summ_names),
caption = "Propiedades estadísticas de los metámeros generados (redondeados a tres cifras significativas).")| \(\overline{x}\) | \(\overline{y}\) | \(S_x\) | \(S_y\) | \(r(x, y)\) |
|---|---|---|---|---|
| 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 9 | 7.5 | 3.32 | 2.03 | 0.816 |
| 9 | 7.5 | 3.32 | 2.03 | 0.816 |
Y usando gganimate se puede visualizar cómo pasar del segundo al tercer cuarteto. Todos los pasos intermedios son metámeros del original.
library(gganimate)
metamers %>%
trim(100) %>%
as.data.frame() %>%
ggplot(aes(x, y)) +
geom_point() +
transition_manual(.metamer)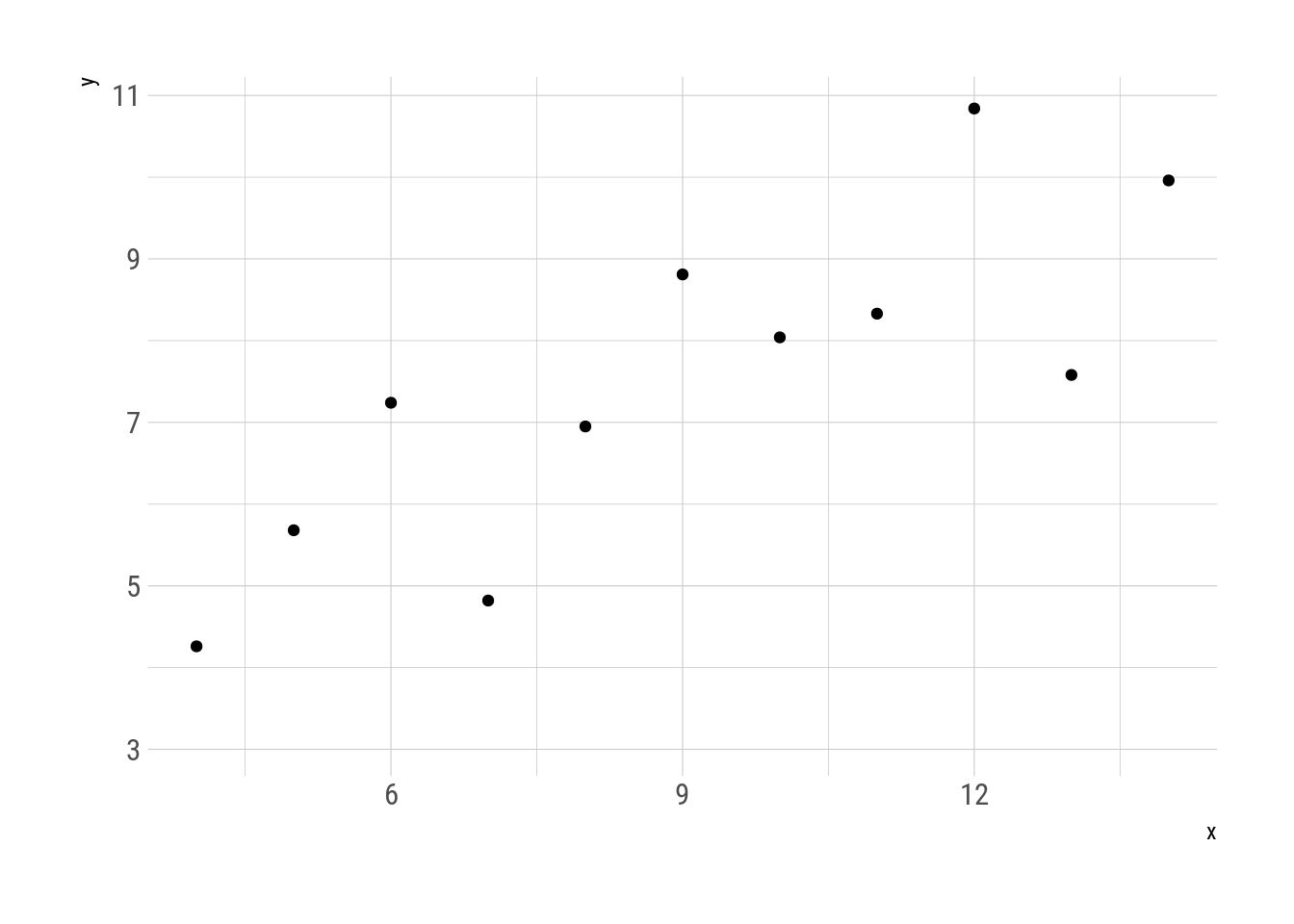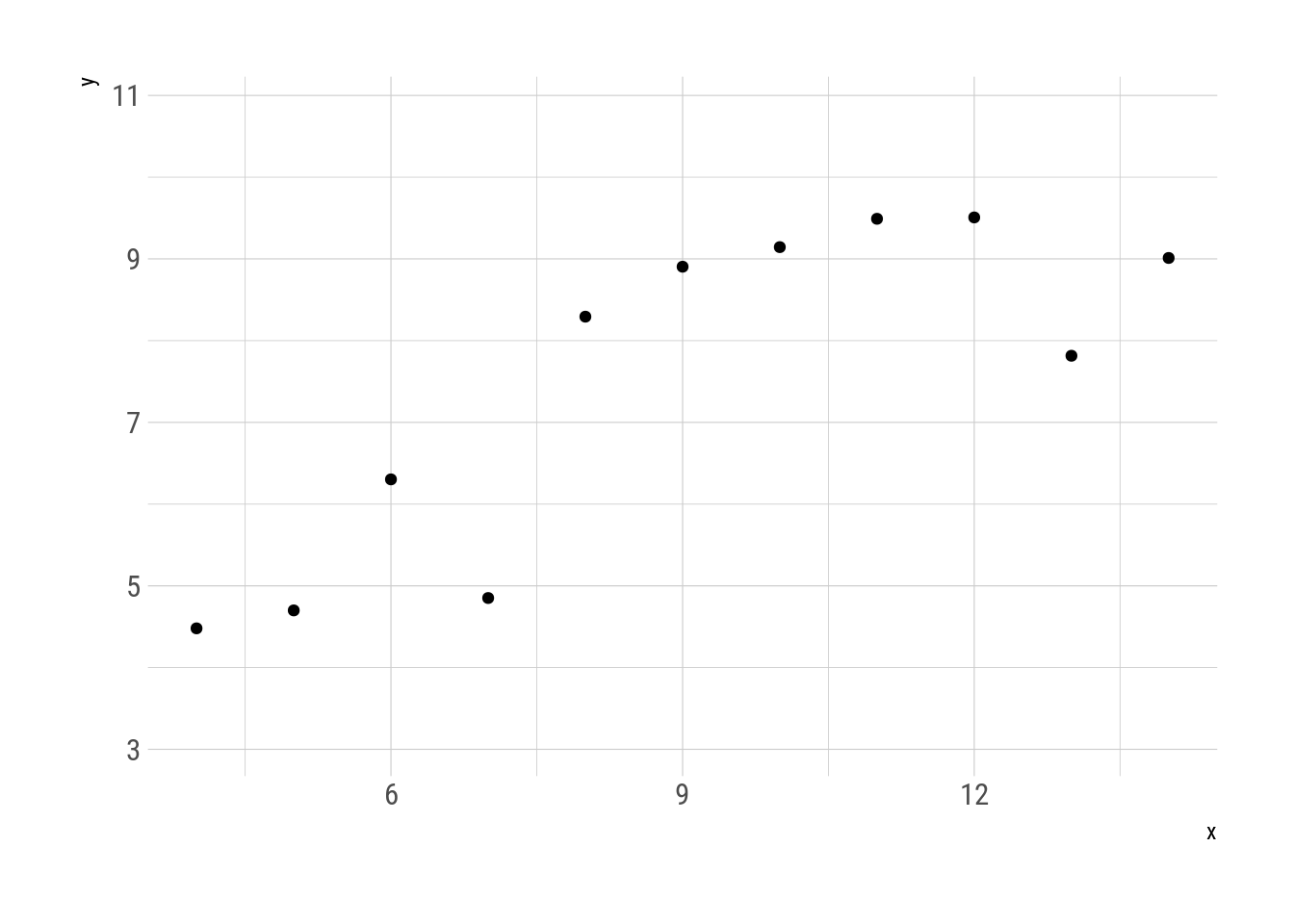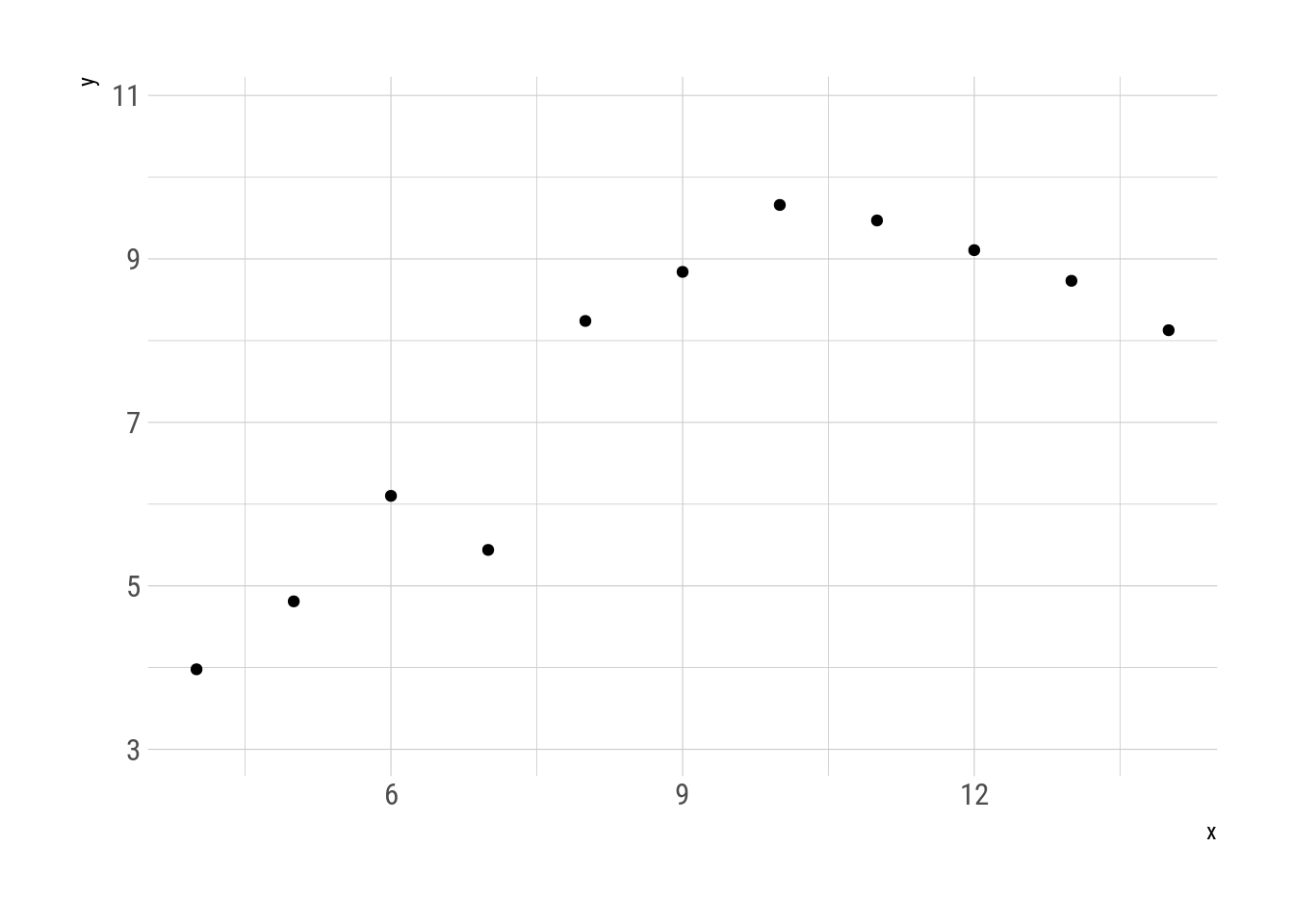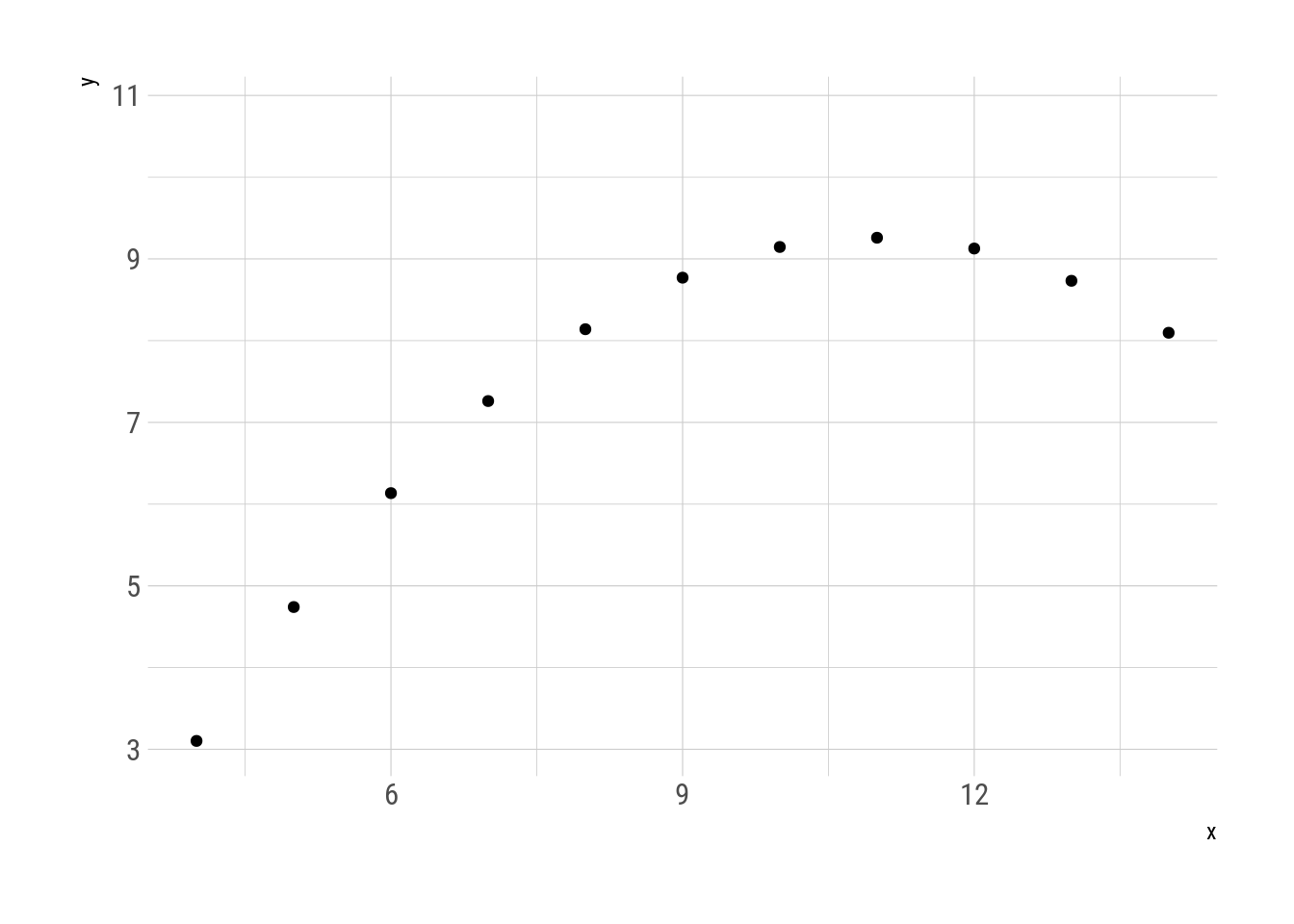
Fig. 3: Transformación del segundo al tercer cuarteto de Anscombe.
En general la discusión alrededor del metamerismo estadístico suele ser sobre la importancia de graficar los datos en vez de únicamente calcular estadísticas resumidas. Anscombe creó su cuarteto para contradecir la idea de que “los cálculos numéricos son exactos, mientras que los gráficos son aproximados”. Actualmente esa es la interpretación que se sigue dando a este fenómeno:
)](../../../images/datasaurus_tweet.png)
Fig. 4: Descargá el Datasaurio: Nunca confíes sólo en las estadísticas resumidas; siempre visualizá tus datos. (Tweet)
Sin embargo, creo que hay un principio más fundamental. El problema de las summary statistics es la parte de summary. El rol de la estadística es, en muchos casos, resumir datos. Tomar una gran cantidad de observaciones que no pueden ser entendidas en su completitud porque nuestro entendimiento es limitado, y reducirlas a unos pocos números o propiedades que podemos entender fácilmente. El problema es que lo que se gana en entendimiento, se pierde información.
Por ejemplo, un censo de los ingresos de todos los ciudadanos de un país tiene una enorme cantidad de información, pero tomados como datos separados dicen poco. Se puede resumir con el promedio (el primer momento) para tener alguna idea del valor “típico” de esta variable. Obviamente, este número esconde una gran desigualdad, por lo que es conveniente usar el desvío estándar (segundo momento) para tener una idea de cuán variable es la distribución del ingreso. Pero es muy probable que la distribución no sea simétrica. Se puede usar la asimetría (tercer momento) para empezar a cuantificar ese efecto.
Cada momento que se agrega permite tener más información sobre los datos crudos. El límite es cuando se tienen tantos momentos como datos en la muestra. Una muestra univariada de tamaño N puede ser descripta unívocamente por sus N primeros momentos. Esto tiene sentido intuitivamente –no se debería necesitar más de N números para describir N números– pero también tiene demostración matemática1.
En otras palabras, la transformación “primeros N momentos de una muestra de tamaño N” no tiene metámeros estadísticos salvo cualquier permutación de la muestra original (pero ver 1).
Esta propiedad no es única de los momentos estadísticos. La transformada de fourier tiene la misma propiedad, lo mismo que las componentes principales, análisis factorial, clustering, etc…2. El problema no es gráficos vs. números sino “todos los números” vs. “sólo algunos números”. La ventaja de los gráficos es que permiten representar gran cantidad de números de una forma eficiente e intuitiva, permitiendo una gestalt que es imposible lograr simplemente mirando una serie de números.
Esta observación permite predecir en qué casos será más fácil encontrar metámeros y cuándo es matemáticamente imposible. Por ejemplo, no se puede encontrar metámeros de una muestra de tamaño 10 que preserve 10 momentos.
set.seed(42)
start_data <- data.frame(x = rnorm(10))
metamerize(start_data,
moments_n(1:10),
signif = 3,
perturbation = 0.05,
N = 30000)## List of 1 metamersPero sí se puede encontrar metámeros que preserven dos momentos.
set.seed(42)
metamerize(start_data,
moments_n(1:2),
signif = 3,
perturbation = 0.01,
N = 30000)## List of 263 metamersUn boxplot representa una muestra mediante unos 5 números, por lo que es esperable que demuestre metamerismo para muestras de \(N>5\). Una estimación de densidad usando métodos paramétricos, en cambio, devuelve potencialmente infinitos puntos a partir de una muestra de cualquier tamaño. La posibilidad de metamerismo en ese caso depende de la “resolución” con la que se describa la curva. Si la curva es descripta con menos puntos que el tamaño de la muestra, va a tener metámeros.
coarse_density <- function(data) {
density(data$x, n = 16)$y
}
set.seed(42)
metamerize(data.frame(x = rnorm(100)),
preserve = coarse_density,
N = 5000,
signif = 3,
perturbation = 0.001)## List of 11 metamersMientras que si se la describe con más puntos, no permite metamerismo.
highdef_density <- function(data) {
density(data$x, n = 200)$y
}
set.seed(42)
metamerize(data.frame(x = rnorm(100)),
preserve = highdef_density,
N = 5000,
signif = 3,
perturbation = 0.001)## List of 1 metamersEste principio general está bien, pero no está completo. Imaginemos una transformación estadística que devuelva un vector de tamaño N con el promedio de una muestra repetido N veces. A pesar de obtener N números a partir de una muestra de tamaño N, tiene la misma información que si fuera sólo el promedio. Generar metámeros para esta transformación es trivial.
mean_n_times <- function(data) {
rep(mean(data$x), length.out = length(data$x))
}
set.seed(42)
metamerize(data.frame(x = rnorm(100)),
preserve = mean_n_times,
perturbation = 0.1,
N = 1000)## List of 43 metamersEsto motiva definir la categoría de transformaciones estadísticas “eficaces” como aquellas que pueden describir una muestra univariada de tamaño N con unicidad a partir de N números o menos. Bajo esta definición, “los primeros N momentos” es una transformación eficaz mientras que “repetir el primer momento N veces” no lo es. Esto, igual es pura especulación mía.
Vale la pena notar que en la búsqueda empírica de metámeros hay que establecer un nivel de exactitud tolerable (con el argumento signif). Si se quiere ser exactos, éstos no son metámeros verdaderos sino más bien “semi-metámeros”. Esta diferencia implica que si se tolera una exactitud baja es posible encontrar (semi)-metámeros aún cuando teóricamente no debería ser posible.
set.seed(42)
metamerize(data.frame(x = rnorm(3)),
moments_n(1:4),
signif = 1,
perturbation = 0.001,
N = 1000)## List of 1000 metamersMetámeros avanzados
Finalmente, me gustaría mostrar algunas utilidades de metamer que facilitan mucho la creación de nuevos metámeros. Con draw_data() uno puede dibujar datos a mano alzada en una interfaz de shiny, opcionalmente usando otra base de datos como fondo.
start_data <- subset(datasauRus::datasaurus_dozen, dataset == "dino")
start_data$dataset <- NULL
smiley <- draw_data(start_data)
simley$.group <- NULL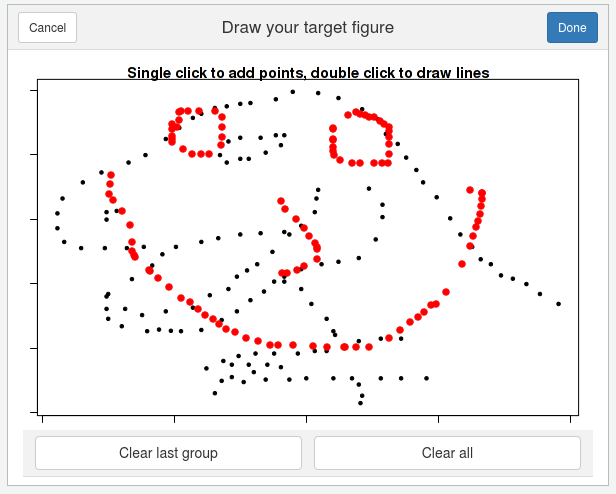
Fig. 5: Interfaz de draw_data().
Además, metamerize() puede encadenarse y guarda los parámetros que se usaron antes, excepto N y trim. De esta forma se puede hacer secuencias.
X <- subset(datasauRus::datasaurus_dozen, dataset == "x_shape")
X$dataset <- NULL
star <- subset(datasauRus::datasaurus_dozen, dataset == "star")
star$dataset <- NULLmetamers <- metamerize(start_data,
preserve = delayed_with(mean(x), mean(y), cor(x, y)),
minimize = mean_dist_to(smiley),
perturbation = 0.08,
N = 30000,
trim = 150) %>%
metamerize(minimize = NULL,
N = 3000, trim = 10) %>%
metamerize(minimize = mean_dist_to(X),
N = 30000, trim = 150) %>%
metamerize(minimize = NULL,
N = 3000, trim = 10) %>%
metamerize(minimize = mean_dist_to(star),
N = 30000, trim = 150) %>%
metamerize(minimize = NULL,
N = 3000, trim = 10) %>%
metamerize(minimize = mean_dist_to(start_data),
N = 30000, trim = 150)Esta serie de metámeros muestra al datasaurio metamorfoseando en distintas figuras, siempre manteniendo las mismas propiedades estadísticas y logrando algo similar a la animación de Justin Matejka y George Fitzmaurice.
metamers %>%
as.data.frame() %>%
ggplot(aes(x, y)) +
geom_point() +
transition_manual(.metamer)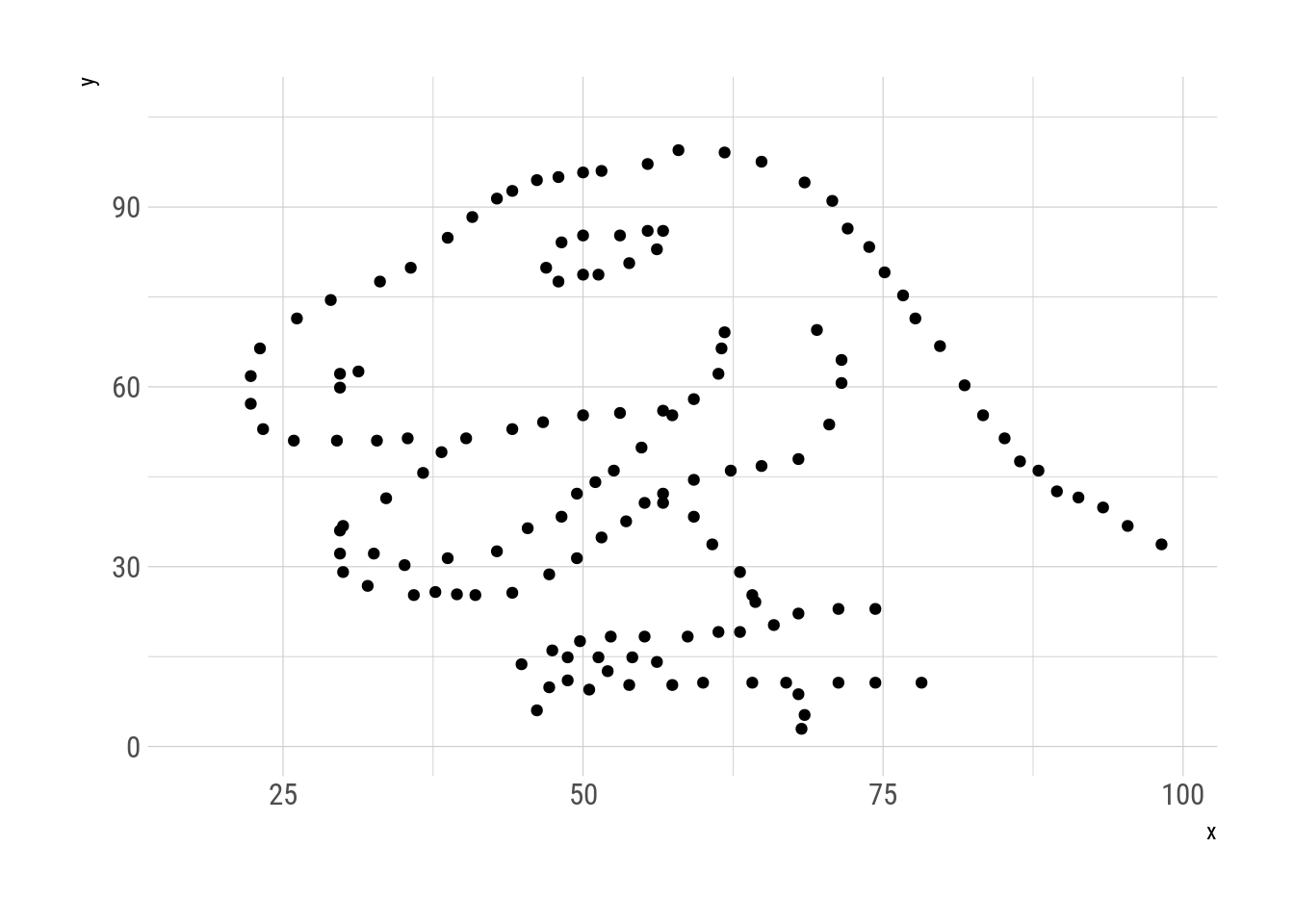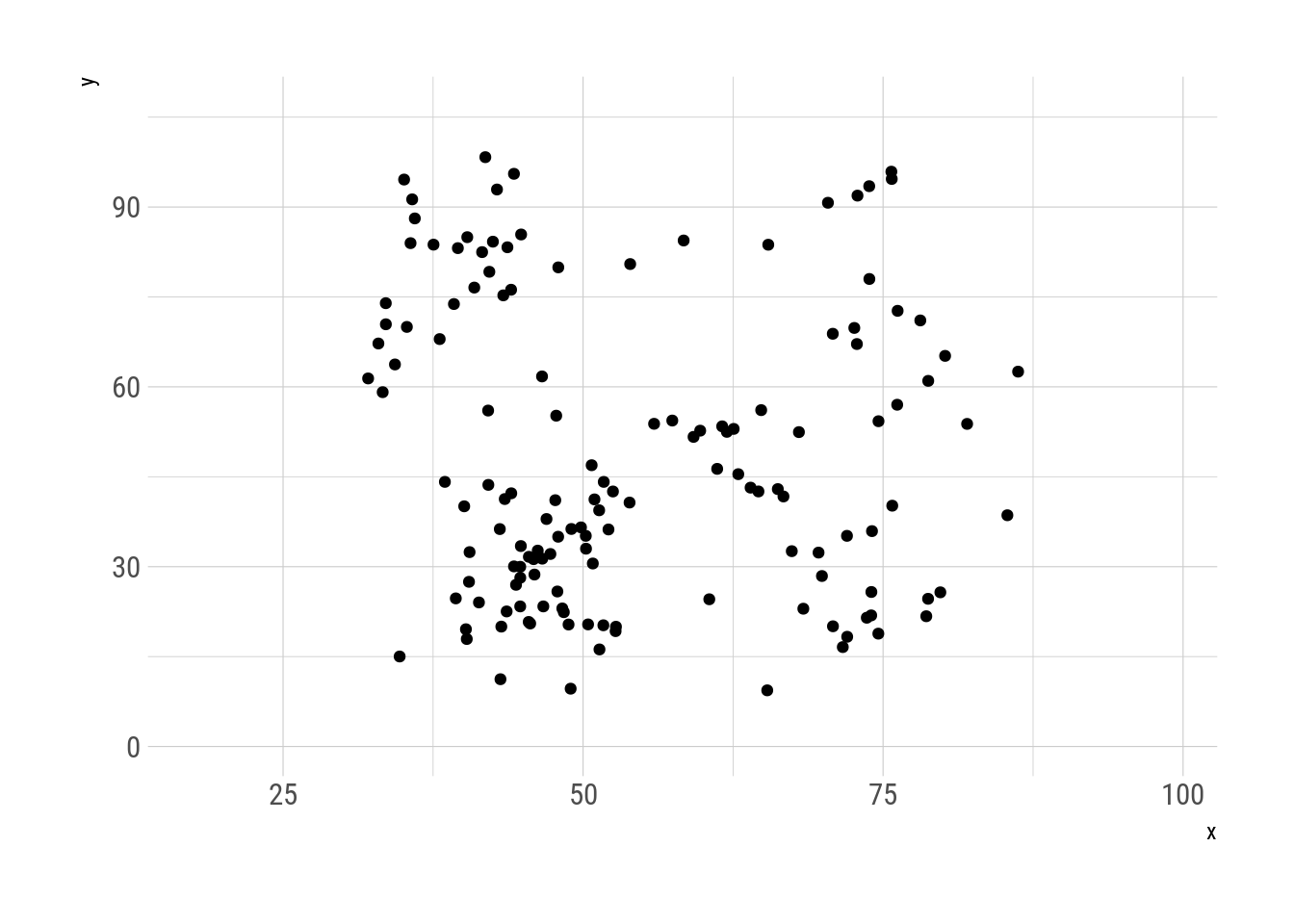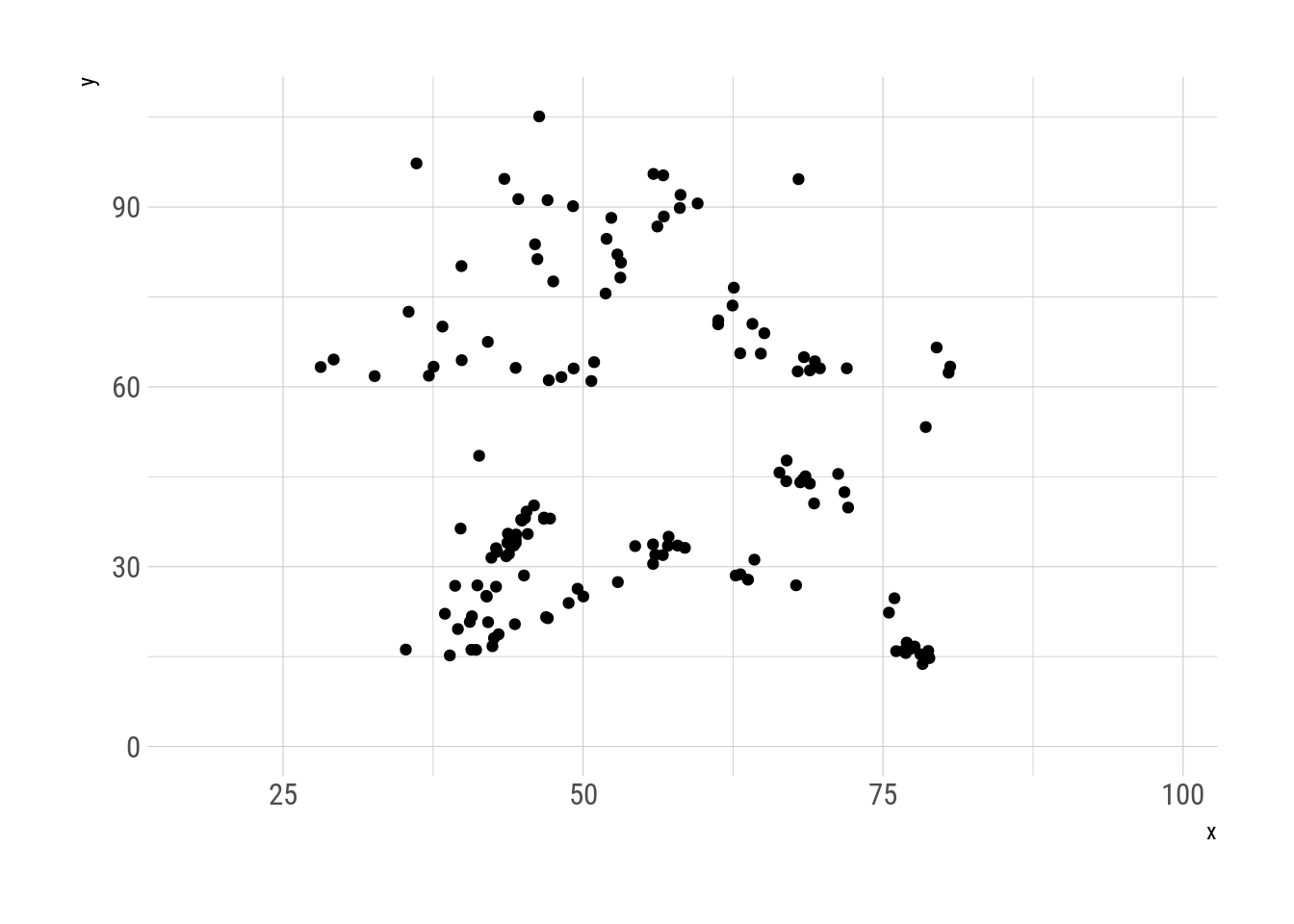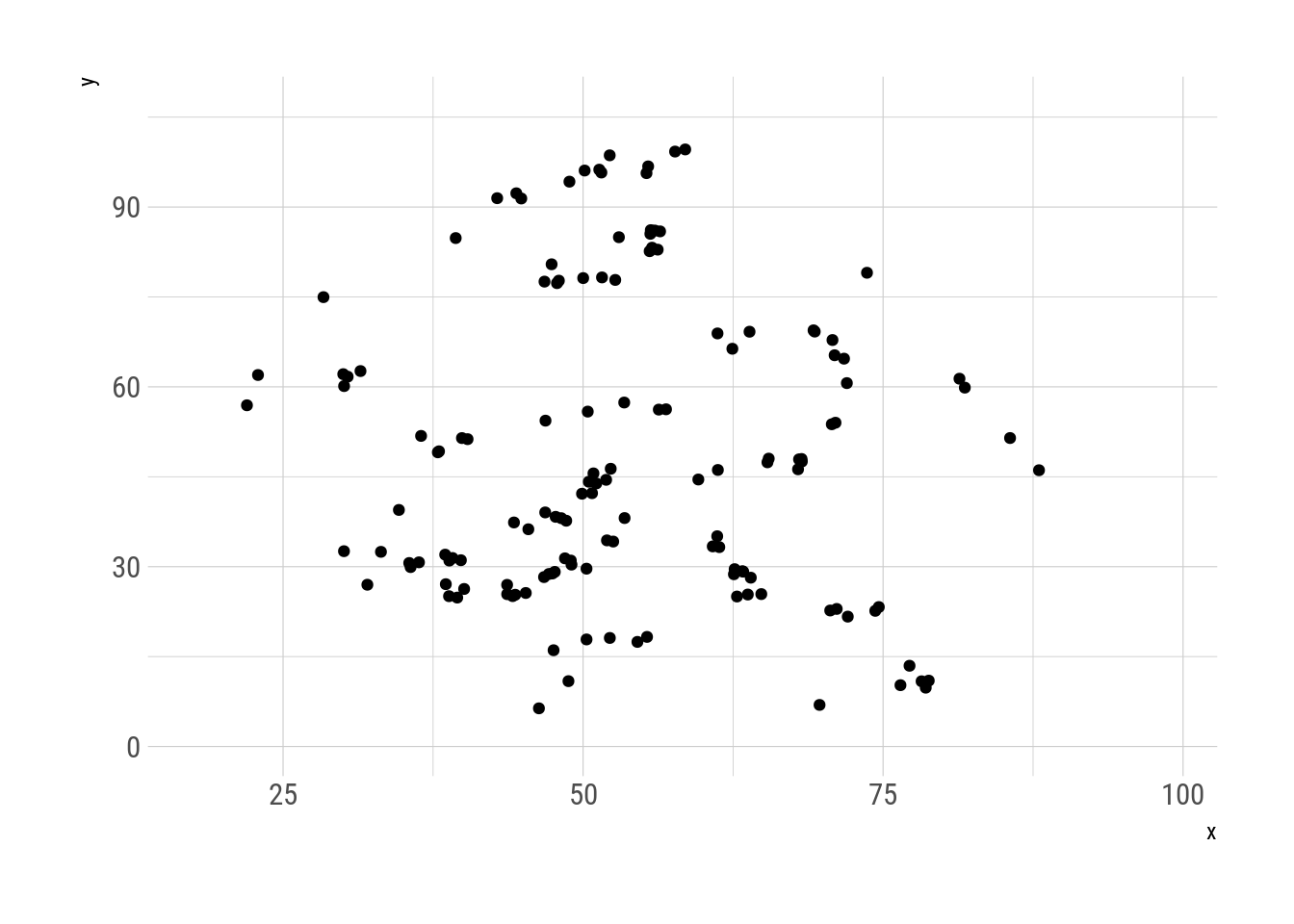
Fig. 6: Metamorfosis del datasaurio.
Referencias
Anscombe, F J. 1973. “Graphs in Statistical Analysis.” The American Statistician 27 (1): 17–21. https://doi.org/10.1007/978-3-540-71915-1_35.
Chatterjee, Sangit, and Aykut Firat. 2007. “Generating data with identical statistics but dissimilar graphics: A follow up to the anscombe dataset.” American Statistician 61 (3): 248–54. https://doi.org/10.1198/000313007X220057.
Govindaraju, K., and S. J. Haslett. 2008. “Illustration of regression towards the means.” International Journal of Mathematical Education in Science and Technology 39 (4): 544–50. https://doi.org/10.1080/00207390701753788.
Haslett, S. J., and K. Govindaraju. 2009. “Cloning data: Generating datasets with exactly the same multiple linear regression fit.” Australian and New Zealand Journal of Statistics 51 (4): 499–503. https://doi.org/10.1111/j.1467-842X.2009.00560.x.
Hunt, R. W. G. 2004. “The Colour Triangle.” In The Reproduction of Colour, 6th ed., 68–91. https://doi.org/10.1002/0470024275.
Matejka, Justin, and George Fitzmaurice. 2017. “Same Stats, Different Graphs.” Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems - CHI ’17, 1290–4. https://doi.org/10.1145/3025453.3025912.
Técnicamente la descripción es única a menos a menos de permutaciones de los valores. Esto no es casualidad. El caso donde el orden de los valores importa es, en realidad, un caso de muestras bivariadas (cada “dato” es un par de valores (x; y)). La intuición es que además de los momentos de cada variable, son necesarios los momentos cruzados (covarianza, etc…). La demostración para el caso multivariado es complicada pero parece que existe, aunque no creo poder entenderla. Por intuición me parece plausible que en ese caso sea necesaria la matriz \(A^{N\times N}\) donde el elemento de la fila \(i\) y columna \(j\) es \(x^iy^j\); lo cual implica necesitar \(N^2 - 1\) momentos.↩
El caso de la transformada de fourier es interesante porque describe una serie ordenada de tamaño \(N\) con dos series ordenadas de \(N/2\) números (una real y otra imaginaria). Es decir, \(2N\) números en total (las dos series y sus respectivos órdenes). Esto es mucho menor que \(N^2-1\) supuesto antes pero sospecho que esto es porque esta propiedad de fourier es para series equiespaciadas. Si los datos tienen alguna restricción, se puede “comprimir” la información.↩
